| | 
Pierre Vernier
|
Pierre Vernier (1584-1638)
MacTutor
|
Wikipedia
|
Galileo Project
|
Encyclopedia Britannica (1911)
French mathematician, military engineer and instrument-maker, born in Ornans (near Besançon,
Franche-Comté, now in France)
where a collège
is named after him
(so is a public institute
for technological innovation, located in Besançon).
Pierre Vernier served the King of Spain who was ruling Franche Comté
at the time.
In 1623, he was awarded the title of citizen of Besançon for his work on the fortifications of the city.
In a treatise entitled
La Construction, l'usage, et les propriétés du quadrant nouveau de mathématiques
(Brussels, 1631) Pierre Vernier published a description of the sliding scale
named after him and used in quadrants,
sextants,
calipers and other precision measuring instruments.
Originally, he described a quadrant allowing
angular measurements
to a precision of one minute, using a main scale graduated in half-degrees and a movable sector
divided into 30 equal intervals spanning 29 half-degrees.
The underlying idea can be traced to the
multiple fixed scales of the nonius
invented by the Portuguese mathematician
Pedro Nunes (1502-1578)
which Tycho Brahe (1546-1601) dismissed as
unpractical (the multiple scales were also difficult to engrave to the required
precision).
Improvements were attempted by
Jacob Curtius (1554-1594)
and by the Bavarian Jesuit
Christopher Clavius
(né Schlussel, 1538-1612)
who is best remembered as the astronomer who engineered the modern
Gregorian calendar.
By replacing the full-length fixed scales of the nonius
with a short movable scale, Pierre Vernier
eliminated the need for auxiliary tables and invented a truly
practical device (which would become popular
early in the eighteenth century).
That innovation was properly named after Vernier by
Lalande in 1771,
but the earlier etymology (nonius) survives in some languages.
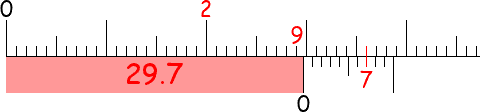
In modern times, the most common Vernier scales are decimal ones,
featuring 10 intervals spanning 9 intervals of the main scale.
If the two scales coincide precisely after n Vernier intervals,
then the measurement exceeds by n/10
whatever is indicated on the main scale (just before the zero of the Vernier scale):
| | 
Ismaël
Bullialdus
|
Ismaël Bouillaud; Bullialdus (1605-1694)
MacTutor
|
Wikipedia
|
SEDS
|
Biblical Cyclopedia
The correct French spelling is Bouillaud with a trailing "d",
as evidenced by the learned Latinized version Bullialdus.
However, that final consonant is silent and the alternate spelling
Bouillau is often found, not only in English texts.
Ismaël Bouillaud was born in
Loudun to French Calvinist parents.
His father was a notaire and an amateur astronomer who was
also called Ismaël (so was an elder sibling who died in infancy).
Ismaël the younger converted to Catholicism at the age of 21 and was ordained
a Catholic priest at the age of 26.
Our subject was an early advocate of some
of the ideas put forth by Copernicus (1473-1543),
Galileo (1564-1642) and
Kepler (1571-1630).
Ismaël Bullialdus didn't accept Kepler's
second law (and never discussed the
third).
He wouldn't use the (correct) description of planetary motion given
by Huygens (1629-1695)
as forward motions curved sideways by the Sun's pull.
(Bullialdus once believed that the force exerted by the Sun was attractive
at aphelion but repulsive at perihelion.)
Nevertheless Bullialdus was credited by
Newton (1643-1727)
for the idea of a central force of gravitation in the
Solar system.
Ismaël Bullialdus had proposed the
inverse-square law
for several physical phenomena, including gravitation, as early as 1645.
He didn't follow through as much as he might have and is thus still mocked as being
the
finder but not the keeper of the inverse-square law.
Yet, his original words were crystal-clear:
As for the power by which the Sun seizes or holds the planets, and which, being corporeal, functions in the manner of hands,
it is emitted in straight lines throughout the whole extent of the world, and like the species of the Sun,
it turns with the body of the Sun; now, seeing that it is corporeal, it becomes weaker and attenuated at a greater distance or interval,
and the ratio of its decrease in strength is the same as in the case of light, namely, the duplicate proportion, but inversely,
of the distances that is:
1 / d 2
In the main, the only dubious part in this was the guess that the gravitational influence of the Sun
would depend on its own rotation. (General relativity later taught us
that such rotational dependence, albeit nonzero, is utterly negligible.)
Bullialdus was duly made a Fellow of the Royal Society on 4 April 1667.
He was a key figure in the informal République des Lettres,
which was bringing about the fermentation and exchange of ideas in
French, mostly through the circulation of handwritten letters.
The network included the likes of
Peiresc (1580-1637)
and Gassendi (1592-1655).
Shortly after the death of Bullialdus, his entire library was dispersed.
His books, manuscripts and correspondence were known as the Archive Boulliau (so spelled).
A major portion of the papers was acquired by the Bibliothèque du Roi sometime before 1782.
Those were later collected in 41 volumes (23000 pages) which now form the
Collection Boulliau at
BNF (FF. 13019-13059).
Another 7000 pages of manuscripts are scattered over some 45 different archives, in a dozen countries.
The Archive Boulliau once had so much prestige that it attracted
a flurry of thieves and forgers,
including Guglielmo
Libri (1803-1869) and the infamous
Denis Vrain-Lucas (1818-1882)
who would defraud Chasles (1793-1880).
Inverse-square law (1645)
|
Astronomia Philolaica (Paris, 1645)
| | 
Robert Hooke
(by Rita Greer, 2004)
|
Robert C. Hooke (1635-1703, FRS 1663)
MacTutor
|
New World
|
Britannica
|
WP
|
Berkeley
|
Robert Hooke Society
[ deeds ]
Born at noon on Saturday, July 18, 1635
(that's July 28 in the Gregorian calendar)
in Freshwater,
on the Isle of Wight.
Youngest child of John Hooke, a curate in charge of
All Saints Church (Freshwater)
and his second wife (1622) Cecelie Gyles, a local merchant's daughter.
They had 4 children: Anne (1623), Katherine (1628), John Jr. (1630) and Robert (1635).
Robert Hooke was at first expected to become a minister himself
(all three of his father's brothers were).
However, his sickly constitution and frequent headaches, hindered Robert's normal schooling
and, eventually, he was pretty much left on his own devices at home.
His depressed father hanged himself in 1648.
The way young Robert was reproducing pictures hanging in his home had impressed a visiting artist,
John Hoskyns, who encouraged him to pursue drawing.
In 1648, Hooke was thus sent to London for an apprenticeship under a prominent portrait painter
of that era, Peter Lely (1618-1680).
However, Robert soon decided that his youth (and a small sum from his father)
would be better spent on a formal education.
John Wilkins (1614-1672)
made him a pupil of Westminster
School, where Robert boarded in the house of the headmaster,
Dr. Richard Busby (1606-1695).
In 1653,
he went to Christ Church, Oxford
on a choral scholarship, learning astronomy from
Seth Ward (1617-1689)
the third Savilian Professor,
future founding member of the Royal Society (1659) and
Bishop of Salisbury (1667).
Wilkins recommended Hooke's mechanical talents to
other scientists belonging to an invisible college of London scientists
meeting at Oxford: Thomas Willis, Robert Boyle, John Wallis,
Christopher Wren and William Petty.
He worked for them as a paid assistant in 1655 and 1656.
Robert Hooke was hired before hefore he could graduate from Oxford:
From 1657 to November 1661, he worked exclusively as the assistant of
Robert Boyle (1627-1691).
His first task was to build a vacuum pump for Boyle.
He also designed a long (4 m) J-tube which allowed a precise verification of
Boyle's law (1662).
In 1660, Hooke first observed the linear variation of tension with extension in an elastic spring.
That's the basic law of elasticity now taught in high-school:
The elongation of a spring is proportional to the force applied to it
(a special case of a general principle Hooke formulated in 1678,
now known as Hooke's law).
By producing a practical way to measure forces in a variety of circumstances,
this freed the force concept from the familiar notion of weight
(which is the force exerted by gravity on any massive body near the surface of the Earth).
C'est pas bien malin.
Lucien Refleu (1975).
In 1661,
King Charles II of England (1630-1685)
commissioned Sir Christopher Wren for a series of microscopical studies of insects.
After accepting the commission, Wren found he lacked the time for the project
and passed it on to Hooke because of his knack for drawing.
On 1 January 1663, out of sheer curiosity, Hooke turned his microscope to thin slices
of cork and he discovered a network of walls surrounding what he immediately termed
pores or cells. The latter term stuck!
In November 1661, Hooke was appointed Curator of Experiments
of the newly-formed Royal Society (formally leaving Boyle's employement).
It was an unpaid position until 1665-01-11; it's unclear whether Boyle supported him in the interim or not.
Hooke would serve in this capacity for over 40 years.
As such, he was responsible for all experiments performed at the Society's weekly meetings.
He was elected FRS in 1663.
In March 1665, the merchants of London appointed Hooke Gresham Professor of Geometry at
Gresham College, London (founded 1597).
A clause in this appointment, forced him to remain a bachelor
(although, unlike Newton, Hooke wouldn't always lead a celibate life).
He had been provided with lodging at the College since 1664 and would live there for the rest of his life.
In 1666, Robert Hooke and Giovanni Alfonso Borelli independently expounded
gravitation as an attractive force, following Bullialdus (1645):
- "On Gravity", lecture by Robert Hooke at the Royal Society (1666-03-21).
- "Theory of the Planets" (1666) by
Alfonso Borelli (1608-1679).
Then, London burned and the course of History was changed...

After the Great Fire of London (September 1666)
Hooke became one of three city surveyors and he undertook personally more than half of the needed surveys
to rebuild the city (partly on old fundations to save money that couldn't be diverted from the
war effort against the Dutch). He supervised the reconstruction with Christopher Wren, until it
was almost done (1674). He became quite wealthy.
In 1670, Hooke gave a lecture at Gresham College
explaining that gravitation applies to all celestiall bodies
and that its strength decreases with distance.
He remarked that, in the absence of gravity, said bodies would move in straight lines.
In 1679, Hooke wrote a letter to Isaac Newton where he
speculated that the strength of gravity might decrease
inversely as the square of the distance.
He later felt that Newton didn't properly credit him or others.
This fueled a bitter feud between the two men.
In all fairness, Newton's
Principia
(1687) does acknowledge that Hooke, along with Wren and Halley,
had separately appreciated the inverse-square law
in the solar system.
Newton also gave credit to Bullialdus for the seminal idea.
In 1678, Hooke published the general principle now known as
Hooke's law
(ut tensio, sic vis):
A disrupted stable equilibrium tends to be restored
by a force directly proportional to the extension therefrom.
Stress and strain are proportional.
It's approximatively so in a multitude of practical cases, including
masses on springs (Hooke, 1660)
and pendulums
(Galileo, 1581).
It's this fight between inertia and restoring forces that creates
simple harmonic motion (at least as a first approximation).
Hooke's health degraded over the last decade of his life and he
died in London on March 3, 1703. Biographical details about him are
mostly due to his two friends
Richard Waller (16??-1715)
and John Aubrey (1626-1697).
Robert Hooke was arguably the greatest experimental scientist
of the 17-th Century. He is credited for:
Missing portrait(s)
|
Accomplishments
|
Discovery of the Cell (1663)
|
Micrographia (1665)
|
Geology
Recent Biographies :
The biography of Robert Hooke by Stephen Inwood (1947-).
is published under two different titles:
"The Man Who Knew Too Much:
The Strange and Inventive Life of Robert Hooke, 1635-1703" (Pan Macmillan, 2002)
"Forgotten Genius:
The Biography of Robert Hooke, 1635-1703" (MacAdam/Cage, 2005)
"The Curious Life of Robert Hooke : The Man Who Measured London"
(HarperCollins, 2003) by Lisa Jardine (1944-2015).
"England's Leonardo: Robert Hooke and the Seventeenth-Century Scientific Revolution"
(Taylor & Francis, 2004) by Allan Chapman (1946-).
For Young Readers :
"Robert Hooke: Creative Genius, Scientist, Inventor"
(Great Minds of Science, 2006) by Mary Gow.
"Robert Hooke: Natural Philosopher and Scientific Explorer"
(Signature Lives, 2007) by Michael Burgan.
Excerpt from Hooke's biography by the late Dr. Lisa Jardine.
April 25, 2004.
The Curious Life of Robert Hooke : The Man Who Measured London
FIRST CHAPTER The Boy from the Isle of Wight
Many other things I long to be at, but I do extremely want time.
Hooke to Robert Boyle, 5 September 1667
On Saturday, 10 April 1697, a little less than five years before his death,
Robert Hooke sat down with 'a small Pocket-Diary', specially purchased for the purpose,
to write his autobiography:
I began this Day to write the History of my own Life,
wherein I will comprize as many remarkable Passages,
as I can now remember or collect out of such Memorials as I have kept in Writing,
or are in the Registers of the Royal Society; together with all my Inventions,
Experiments, Discoveries, Discourses, &c. which I have made, the time when,
the manner how, and means by which, with the success and effect of them,
together with the state of my Health, my Employments and Studies,
my good or bad Fortune, my Friends and Enemies, &c.
all which shall be the truth of Matter of Fact,
so far as I can be inform'd by my Memorials or my own Memory,
which Rule I resolve not to transgress.
And there, to all intents and purposes, he broke off. [ ... ]
All that Hooke's literary executor
Richard Waller
found among his old friend's personal papers to flesh out the skeletal autobiography
was a few schematic paragraphs about Hooke's boyhood and early life.
They begin:
Dr. Robert Hooke was Born at Freshwater, a Peninsula on the West side of the Isle of Wight,
on the eighteenth of July, being Saturday, 1635, at twelve a Clock at Noon,
and Christened the twenty sixth following by his own Father, Minister of that Parish.
| | 
James Bradley
|
James Bradley (1693-1762)
Britannica
|
Wikipedia
|
MacTutor
|
Select Surnames
James Bradley was born
in Sherborne, Gloucestershire, but his family still owned
the ancestral Bradley Castle near the market
town of Wolsingham
in County
Durham.
That land had been in the family for centuries.
E.g., Roger de Bradley (1183). William de Bradley (1341).
-
[2] Father : William Bradley (b.1640)
-
[3] Mother : Jane Pound (born in 1656, married in 1678).
-
[1] Siblings :
| | 
Guillaume Rouelle
|
Guillaume François Rouelle (1703-1770)
Wikipedia
|
Wikipédia (French)
|
France pittoresque
Guillaume Rouelle was born on September 16, 1703
to a farming family near Caen,
in the village of Mathieu,
reputedly the birthplace of the famous poet
François de Malherbe (1555-1628)
after whom would be named, in 1892, the Lycée
of Caen (which still hosts the Taupe Laplace).
Guillaume was the oldest of 12 children.
His younger brother Hilaire Rouelle (1713-1779)
also became a chemist and is credited for independently discovering
urea in 1773
(although Herman Boerhaave (1668-1738)
had isolated it from urine as early as 1727).
The two brothers are known in chemical literature as l'aîné
and le cadet (i.e., the Elder and the Younger).
After starting medical school in Caen (at
Collège du Bois)
Guillaume went to Paris where he specialized in pharmacy.
From 1725 to 1732, Rouelle was apprenticed in Paris,
in what had been the laboratory of the famous chemist
Nicolas Lémery (1645-1715)
under the direction of Lémery's successor,
the German apothecary Johann Gottlob Spitzley (1690-1750).
In his spare time, Rouelle kept studying botany and drew the attention of
the leading botanists Antoine & Bernard
de Jussieu, who mentored him.
In 1738, Rouelle established his own
apothecary shop
near place Maubert
(la Maube, an infamous location of public tortures and executions).
He started teaching chemistry privately and his class acquired a solid international reputation.
In 1742, he became professor of chemistry at
Jardin des Plantes
(then called Jardin du Roi).
He was elected to the French Académie des sciences in 1744.
Rouelle firmly supported the variant of
phlogiston theory
put forth in 1703 by
Georg Ernst Stahl (1659-1734).
This had been introduced in France by
Geoffroy the Elder (1672-1731)
whose lectures at Jardin du Roi
were published as Nouveau cours de Chymie in 1723,
when Rouelle was still a student.
In 1754, Rouelle formally defined a base as any chemical substance which
could neutralize
an acid to form a salt.
(Thus generalizing the theories of alkalis and acids
formulated by Lémery in 1680.)
Most chemists and a few luminaries of the era attended the lectures and chemical
demonstrations which Rouelle put forth from 1742 to 1764, including:
He resigned on account of ill-health in 1768 and died in Passy,
on 1770-08-03.
Abbé Joseph-François Marie (1738-1801)
BNF
|
Wikipedia
Born in Rodez (France) on 1738-11-25.
Died in Memel (Germany) in 1801.
He revised and augmented several influential mathematics textbooks by his senior colleague et
Collège Mazarin, l'abbé
Nicolas-Louis de La Caille (1713-1762).
L'abbé Marie taught mathematics at Collège Mazarin
(Collège des Quatre-Nations)
where his star student was Adrien-Marie Legendre (1752-1833).
Several essays by the young Legendre were published in Marie's
own treatise on mechanics (1774). Legendre didn't want his name printed there
but Marie did use the book to bring attention to his former pupil (who had graduated in 1770).
Traité
de Mécanique (1774)
Etienne Midy (c. 1775, fl. 1846)
Midy's theorem (1835)
|
Midy à quatorze heures
(Forum in French, 2010)
His name is spelled Meidy in some records.
He was probably already teaching when Napoléon
instituted the lycées, in 1802.
Midy himself advertised he had taught mathématiques spéciales
at Cahors (1821-1826) and
Orléans (1826-1832) before moving to Nantes.
At the Collège Royal de Nantes
(future Lycée Clémenceau)
Midy taught mathématiques élémentaires
from 1833 to 1837.
That post was entrusted to a young normalien
(Alexandre Lepord, ENS 1834)
when Midy was promoted to teach
mathématiques spéciales again in 1837-1838
(after M. Dorveau resigned).
Midy would be replaced in this capacity by M. Gascheau (previously, professor of physics)
when a ministerial decree (1838-11-17) allowed him to retire.
In Nantes, Etienne Midy lived 3, rue Richebourg,
next to his workplace.
"De quelques propriétés des nombres et des fractions décimales périodiques"
(Forest, Nantes, 1835). 21 pages.
"Du théorème
de M. Sturm et de ses applications numériques" (Nantes & Paris, 1836)
After his retirement in 1838, Etienne Midy published
15 times,
from 1842 to 1846, in
Nouvelles Annales de mathématiques
(Journal des candidats aux écoles Polytechnique et Normale).
"La Conchoïde" 9, 2, pp. 281-292 (1843)
|
"Note sur le folium de Descartes"
1, 3, pp. 293-303 (1844)
"Analyse indéterminée du premier degré" pp. 146-
&
"Equations polaires" pp. 597-, 4 (1845)
"Sur une propriété des nombres" pp. 640-646, 1, 5 (1846)
| | 
Pierre Louis Dulong
|
Pierre Louis Dulong (1785-1838; X1801)

Wikipedia
|
Encyclopedia Britannica (1911)
An only child born in Rouen and orphaned at the age of 4,
Dulong was brought up by an aunt.
He was educated at Centrale-Auxerre and Centrale-Rouen.
He entered Polytechnique
at the age of 16.
He became a physician and worked as a chemist with
Berthollet in Arcueil.
Dulong discovered the explosive properties of nitrogen chloride in 1811,
losing an eye and two fingers in the process.
He worked as a répétiteur
(scientific coach) at the
Ecole Normale Supérieure and was a chemical
technician at Polytechnique under
Louis
Jacques Thénard (1777-1857) a famous teacher who had invented
cobalt blue
in 1802 (that pigment
is still known as Thénard's blue or
bleu de Thénard ).
Dulong was an examiner for the entrance exam of Polytechnique (1813).
He taught physics at the veterinary school of Maison-Alfort until 1827.
In 1820, Dulong and Berzelius determined that water was an oxide of hydrogen.
After the death of Alexis Petit (1791-1820)
Dulong held the chair of physics at
Polytechnique from 1820 to 1829.
He was thus the third holder of the chair of physics at Polytechnique,
following Hassenfratz (1794) and
Petit (1815).
A second chair of physics would be created for
Jules Jamin (1818-1886)
who taught at Polytechnique from 1852 to 1881.
The sixth holder of that second chair, from 1936 to 1969,
was Louis Leprince-Ringuet (1901-2000; X1920N)
who was instrumental in obtaining the creation, in 1958,
of a third chair of physics at Polytechnique for
Bernard P. Grégory (1919-1977; X1939)
who would become director-general at CERN (from 1965 to 1970) after the retirement of
Viki Weisskopf (1908-2002).
For his joint work with Petit (including the formulation of the
Dulong-Petit law,
in 1819) Dulong was elected to the physics section of the French
Académie des sciences
(of which he would become president, in 1828).
Dulong was director of scientific studies at Polytechnique from 1830 to 1838.
His successor in this capacity was
Gustave Coriolis (1792-1843; X1808).
Ma tre de conférences à Normale (1830),
il est professeur de chimie en Sorbonne (1832).
Il fut membre de l'Académie de médecine.
Les "Lois de Dulong" ont fondé l'analyse des minerais insolubles.
Il étudie la force élastique des vapeurs et la loi de Mariotte,
imagine le cathétomètre et le thermomètre à poids.
Dulong et Arago formulent la loi sur les machines à vapeur
demandée par le gouvernement en 1825.
--- Refer. : Dbf 12, 83 (bibliogr.) - Larousse 2, 992-3 (gr.) - LC 1, 269-85 (méd.)
| | 
Jacques Babinet
|
 Jacques Babinet (1794-1872; X1812)
Jacques Babinet (1794-1872; X1812)
Christian Nitschelm |
Wikipedia
Jacques Babinet was born on 1794-03-05 in
Lusignan (Vienne)
to Jean Babinet, mayor of Lusignan, and his wife Marie-Anne Félicité
Bonneau du Chesne, daughter of a lieutenant-general.
He attended the Lycée Napoléon
(formerly Ecole Centrale du Panthéon,
currently Lycée
Henri IV) where he studied under Jacques
Binet (1786-1856; X1804) to prepare for Polytechnique,
which he duly entered in 1812. (Babinet would later become an examiner there.)
After a one-year initial formation at Polytechnique,
Babinet chose to specialize as an artillery officer and went through the
Ecole
militaire de Metz (1813) before being briefly assigned to the
Fifth regiment of Artillery, in Strasbourg.
At the Restoration (1814) he left the Army to become a teacher.
He was professor of mathematics in
Fontenay-le-Comte and
professor of physics in Poitiers
(near his birthplace)
before being awarded the chair of physics at
Saint-Louis in 1820.
From 1825 to 1828, Babinet delivered a course of lectures on meteorology,
including meteorological optics, at ???
In 1838, he succeeded
Félix Savary
(1797-1841; X1815) at the Collège de France.
In 1840, Jacques Babinet was elected to the
Académie des sciences (General Physics section).
The primary focus of his research was the study of diffraction,
which he used to measure wavelengths more accurately than ever before.
In 1827, he proposed a standardization of the ångstrom
based on the wavelength of the prominent red Cadmium line.
(Babinet's idea was used to define the meter, between 1960 and 1983,
in terms of the wavelength of a ray in the spectrum of Krypton.)
He also constructed a hygrometer and improved the valves of air pumps to
achieve a high vacuum.
Jacques Babinet achieved considerable fame as a popularizer of science,
in public lectures and popular articles on a wide range of topics:
geology, mineralogy, astronomy, meteorology...
He passed away in Paris on 1872-10-21, at 78.
Jean Hippolyte Verron-Vernier (1800-1875)
Thèse
de mécanique (1824)
Hippolyte Vernier made his mark as an elite teacher.
In particular, he was the very first mathematics instructor
Evariste Galois ever had (starting in February 1827).
At the time, Vernier was boldly shunning Euclidean
tradition in favor of Legendre's textbook
Elements de Géometrie (1794).
Verron-Vernier entered the
Ecole
Normale Supérieure in 1817.
(Well, it was just called Ecole Normale in those days.)
He was one of only three scientists to do so that year.
The other two were Joseph Avignon (1799-1867)
and [Henri] Jean Adolphe Faure (1799-1879) about whom
little is known.
Upon graduation, in 1820,
he was named
agrégé en mathématiques élémentaires à Angers.
This was the year before the
agrégation of French professors became a national
competition (it still is).
Vernier's direct appointment to teach high-school seniors indicates that he was highly esteemed.
His classmate, Joseph Avignon was likewise appointed in Caen at that same time,
to teach science to high-school seniors and also physics to
mathématiques spéciales students.
When Avignon moved on two years later (1822-11-09) Vernier succeeded him in that position at the
Collège Royal of Caen,
where he made time to write his doctoral dissertation.
In his doctoral thesis entitled
"Distribution de l'électricité à la surface des corps conducteurs"
(July 1824) he made a modest extension
to three spheres of a two-sphere result recently obtained by Poisson.
His doctoral examination committee comprised Poisson himself,
Cauchy and
Lacroix,
among others.
By the time he was appointed to Louis-le-Grand (1826)
Vernier had made several other publications at the research level
(analysis, electrostatics, mechanics, astronomy).
A few months later, the young Galois walked into his class...
In October 1835, Véron-Vernier was promoted to the chair
of mathématiques spéciales at
Henri IV to replace M. Navarre (himself
agrégé in 1811
and promoted inspecteur d'académie for Paris).
Later in his career, Véron-Vernier became a popular writer of textbooks for primary and
secondary education (weights & measures, arithmetic, geometry).
He married M. Neveu in Paris, after 1850.
When he passed away in 1875, the official title of Véron-Vernier was
inspecteur honoraire d'académie à Paris.
He had been inspecteur d'académie at Melun, covering
Seine-et-Marne.
According to a
fantastic
literary legend,
possibly a hoax with some
elements
of truth, Hippolyte fathered a mysteriously plagiarized poet called Hugo Vernier
(1836-1864) born to Sarah Judith Singer on September 3, 1836 in
Vimy.
Legend has it that Hugo Vernier secretly married (1863) Virginie Huet,
a beautiful pianist who was the younger sister of Honorine Huet,
a well-known overweight French spiritualist
(Théophile Gautier
hired first Honorine then Virginie as preceptors for his daughters,
Estelle and Judith).
Hugo Vernier died a few months before Virginie gave birth to a little Vincent, in
Vernon, late in 1864...
The legend is still afloat to this day !
Pierce Morton
(1803-1859)
Proof
of the focus-directrix characterization of conics, using Dandelin spheres
|
Genealogy
Pierce Morton was born on 27 November 1803 in
County Cavan, Ireland.
At Cambridge, he was a pupil of
George Biddell Airy (1801-1892)
who described him as
"a clever gentlemanly man, and a high
wrangler,
but somewhat flighty".
Around 1825, he was appointed Professor of Mathematics and Natural Philosophy
and also Fellow of King's College in Nova Scotia (Canada).
He left the Province suddenly in April 1826.
In the first volume of the
Cambridge Philosophical Transactions (1829)
Morton published a new proof of the focus-directrix property of
conic sections using
Dandelin spheres.
Earlier on, Hamilton (1805-1865) had remarked
that the circle where a Dandelin sphere touches the cone defines a plane whose
intersection with the plane of section is a directrix of the curve.
On 1 June 1839, Pierce Morton married an Irish lady,
Louisa Somerville (1808-1850)
in St. Peter's Church (Dublin, Ireland). They had four children:
-
Frances Armytage Morton was born in 1840.
She married Henry Meredith Cruise
on 26 September 1857 in Anglesey, Wales
(they had a son, named Meredith II, around 1860).
Widowed, she married Mr. Brown in 1878.
Later court documents (Morton's Trusts,
3 March 1888,
pp. 310-313) refer to her as Mrs. Frances McDonald Brown.
Her nickname was Fanny.
-
Pierce Edward Morton (a.k.a. Pierce Junior )
was born on 3 February 1842, in Le Havre
(France) where his father was teaching.
He served as a Midshipman in the Royal Navy, before moving from Cape Town
to Canada, in the autumn of 1860.
He was living in the household of his uncle Dr. Edward Morton,
in East Gwillimbury,
at the time of the 1861 Census.
He drowned with two other people on
August 12, 1861
in the shipwreck of the yacht Wave at
"the Eastern Gap off the Island, Toronto"
(according to a note written by his cousin in the family bible).
-
John D'Arcy Morton was born on 10 January 1843.
-
Arthur Pratt Winter Morton
was born in 1844 and died in 1871, leaving a widow and two children.
All four children were born in France as British subjects.
At the time of the 1851
census of Wales, they were living as wards in William Griffith's home
(in Holyhead, Anglesey).
Their father was living nearby at the time, but he was planning a move to South Africa...
Airy was instrumental in having Pierce Morton sent
as Magnetic Assistant to the Cape Observatory.
Morton arrived in South Africa on November 27, 1851.
He passed away on April 18, 1859 and was
buried in the Cape.
Pierce Morton is listed as the head of the Morton of Kilnacrott family
in Burke's Landed Gentry.
He was one of the 14
children of Charles Carr Morton and Charlotte Tatlow.
His paternal grandfather was the physician
Charles Morton (1716-1799)
principal librarian
of the British Museum from 1776 to 1799.
In the orthodox blazoning style which forbids repetitions of tinctures,
the description of their coat-of-arms is quite convoluted (the punctuation is mine):
Ermine,
on a chevron, between three ogresses,
each charged with a martlet of the field,
as many mascles Or, a chief, Gules.
My understanding is that the field and the three martlets are Ermine, the ogresses are Sable,
the chevron and the chief are Gules and the three mascles are Or.
Geometry,
Plane, Solid, And Spherical, In Six Books (1830) by Pierce Morton & S.W. Waud.
Etienne Bigourdan (1804-1865)
Etienne Bigourdan was born on 10 December 1804 in
Fleurance, Gers.
He died in 1865, probably in Paris.
Bigourdan was neither a normalien nor a polytechnicien.
He dedicated his doctoral work to a normalien (1813, agrégé in 1816):
[Servien Abailard] Armand Lévy (1795-1841)
maître de conférence à l'Ecole Normale (1831-) and
professeur de mathématiques élémentaires (1831-1841) at
Collège Charlemagne.
Bigourdan was awarded his agrégation on 1832-09-24 (ranked third in France)
shortly after obtaining his doctorate in Paris, on
1832-08-13
(which is quite unusual) defending the following set of three theses
(spanning 23 pages)
in front of a committee presided by the chemist
Louis-Jacques Thénard (1777-1857).
1. Equation de la surface capillaire.
2. Composition intérieure des fluides.
3. Sur les éléments d'un sphéroïde.
Etienne Bigourdan served as professeur agrégé
at Louis-le-Grand (c. 1836)
and professeur de physique in Limoges (-1840) just before his promotion to
mathématiques spéciales in Rennes (1840-1842) and
Rouen (1842).
He is correspondant de l'Académie des Sciences in 1847
(listed as professeur de mathématiques spéciales à Paris).
In the later part of his academic career, Bigourdan would fall back to less prestigious positions in
mathématiques élémentaires at
lycée Saint-Louis (-1852)
and, finally, at lycée
impérial Bonaparte (1852-1865).
Guillaume Bigourdan (1851-1932)
was an unrelated French astronomer who famously invented a procedure for setting up a telescope (Bigourdan method).
Et.
Bigourdan à P.-F. Dubois (25 octobre 1840). Letters addressed to Paul-Franç Dubois sous Louis-Philippe.
| | 
Urbain Le Verrier
|
 Urbain Le Verrier (1811-1877; X1831)
Urbain Le Verrier (1811-1877; X1831)
MacTutor
|
Wikipedia
|
Britannica
|
Collège Royal de Caen (1827-1830)
Urbain le Verrier discovered the planet
Neptune
at the tip of his pen (as Arago would later say)
in August 1846, by deducing its position from the recorded perturbations in the orbit of
Uranus. He was also the founder of French meteorology.
From 1827 to 1830,
Le Verrier prepared for the Polytechnique entrance exam
at the Royal College of Caen, when the headmaster was
Jacques-Louis Daniel
(1794-1862, future
recteur
of Caen and bishop of Coutances). His professor of mathematics was
Antoine François Donat Bonnaire (1777-1839) whose son
Charles Antoine Donat Bonnaire (1799-1886; X1819) taught him physics.
Although Urbain was the most brilliant student of his class in Caen, he failed in the
Polytechnique entrance competition of 1830.
His father then decided to sell the family home in Saint-Lô to pay
for tuition at a fancy preparatory school in Paris
(Institution Mayer)
which allowed Urbain to succeed in 1831.
The Institution Mayer had been founded in 1824 by
Mathias Mayer-d'Almbert (1786-1843; X1805)
and it employed the mathematician
Charles Choquet, who would later become
Urbain Le Verrier's father-in-law :
Charles-Adrien Choquet
(1798-1880) had been a mathematical coach
at La Flèche
and he would later obtain a
doctorate in astronomy
(1842).
Mayer and Choquet published three editions (1832,1836,1841) of their
Traité élémentaire d'algèbre
which Choquet updated twice (1845,1849) after the death of Mayer.
Then, he wrote under his own name two editions of a complement (1851,1853)
and a consolidated version with a simpler title:
Traité d'algèbre (1856).
All edited by the dominant French scientific publisher of the era,
Mallet-Bachelier
(called Gauthier-Villars after 1864 and
acquired by Dunod in 1971).
Charles Choquet came from a family of renowned painters and engravers
established in Abbeville,
including his father (or uncle?)
Pierre, Jean-Baptiste, Isidore Choquet (1774-1824)
and his grandfather
Pierre-Adrien Choquet (1743-1813).
All Mayer boarders were auditing classes at Louis-le-Grand,
so that Urbain Le Verrier was taught by the legendary
Louis Richard (1795-1849)
professor at Louis-le-Grand (from 1822 till his death)
whose students have included the likes of
Evariste Galois (1811-1832),
Joseph Serret (1819-1885; X1838)
and Charles Hermite (1822-1901; X1842).
In 1837, Urbain Le Verrier married Lucile Marie Clotilde Choquet,
(the only daughter of his former teacher Charles Choquet). They had
3 children.
Their two sons became polytechniciens too:
Jean Charles Léon Le Verrier (1838-1875; X1856)
and Louis Paul Urbain Le Verrier (1848-1905; X1867).
So did a grandson of theirs (son of the latter)
Pierre Victor Joseph Le Verrier (1882-1964; X1902).
Their daughter Geneviève Joséphine Lucile Le Verrier (1853-1931)
was a talented pianist who studied under
César Franck (1822-1890).
Discovery of Neptune
|
Heraldry:
Roma
|
72 names on the Eiffel Tower

Evariste Galois (1811-1832)
MacTutor
|
The Evariste Galois Archive
|
Math93
|
Fictionalization
|
Stamp
At the age of 20, Evariste Galois
was mortally wounded in a duel (against
Perscheux d'Herbinville,
not
Ernest Duchâtelet)
over a young lady called
Stéphanie-Félice Poterin du Motel.
Left for dead, Galois (who had no
seconds)
was discovered by a local peasant
and transported to the Cochin hospital in Paris,
where he died from peritonitis the next day (May 31, 1832).
To his brother Alfred, he had whispered:
Ne pleure pas, Alfred.
J'ai besoin de tout mon courage pour mourir à 20 ans.
Please don't cry, Alfred. I need all my courage to die at twenty.
Held on June 2, the funerals of Galois were attended by more than 2000 people and served
as a focal point of republican riots which lasted for several days.
His dubious status as a martyred activist could have remained Galois' main claim
to fame had it not been for his wish to have his last mathematical papers reviewed by
Gauss or Jacobi... His brother, Alfred Galois
and his closest friend Auguste Chevalier
did send out copies of the work, which were apparently ignored by
the originally intended recipients.
In 1842, one of these copies reached
Joseph
Liouville (1809-1882) who finally published
what is now known as Galois Theory, in 1846.
The story is poignant enough as it is, but some biographers are perpetuating the
myth that Galois wrote feverishly all he knew about
Group Theory on the night before the fateful duel, apologizing again and
again for not having the time to do it better...
The leading offender is clearly E.T. Bell (1883-1960) who wrote an emphatic chapter
in his popular 1937 collection of biographies entitled
Men of Mathematics.
Actually, there's only one occurrence of such a statement
in all the mathematical manuscripts of Galois
(an "author's note" about an incomplete proof).
Otherwise, the myth seems entirely based on the following sentence which appears in the
letter known as "Galois' Testament",
dated May 29, 1832 and addressed to his friend Auguste Chevalier.
The passage is about extending ambiguity theory
(Galois theory) from rational to transcendental functions.
Mais je n'ai pas le temps,
et mes idées ne sont pas encore
bien développées
sur ce terrain, qui est immense.
But I am running out of time, and my ideas are not yet
sufficiently developed
in this field, which is immense.
Galois' Testament ends with the following words:
Tu prieras publiquement Jacobi ou
Gauss de donner leur avis
non
sur la vérité, mais sur l'importance des
théorèmes.
Après cela il se trouvera, j'espère, des gens qui trouveront leur profit
à
déchiffrer tout ce gâchis.
Je t'embrasse avec effusion. E. Galois, le 29 Mai 1832
|
Until the age of 12, Galois had been schooled entirely by his mother,
Adélaïde-Marie Demante-Galois.
Galois was then enrolled at Louis-le-Grand
(the most prestigious lycée of Paris)
as a boarder in the quatrième grade,
on 6 October 1823 (or 1 April 1824, according to one Louis-le-Grand record).
For the first couple of years, Galois showed no particular interest for
mathematics, in the class taught by Charles Camus (1797-1865).
Born in "Sailly-Zèle" (Somme) Charles Louis Constant Camus
had entered Polytechnique in 1815 and placed third in the
scientific Agrégation for 1821
(which was the first year it took the form of a national competition).
Galois became enthralled with mathematics only in February 1827,
thanks to an exceptional instructor,
Hippolyte Vernier, who had
decided to teach from Legendre's
Elements de Géometrie (1794).
That textbook was then spearheading the liberation
from traditional Euclidean teaching in Europe.
Legend has it that Galois read the textbook in two days. After that, he neglected all other subjects.
In 1828-1829, Evariste Galois was a
Mathématiques Spéciales student
under Louis
Richard (1795-1849) at Louis-le-Grand.
Although he never published anything himself, Louis Richard (1795-1849)
was an outstanding teacher of mathematics, in the French
Grandes Ecoles tradition which is still enduring to this day
(see Lucien Refleu, 1920-2005).
Besides Galois, Louis Richard also taught
Urbain Le Verrier (1811-1877; X1831),
Joseph
Serret (1819-1885; X1838) and, above all,
Charles Hermite (1822-1901; X1842)
whom Richard saw as most similar to Galois and who would go on to achieve the
long, brilliant and prestigious career of which Galois had been deprived
by a stupid early death.
(Hermite also had a lasting impact by teaching the likes
of Jules Tannery and
Henri Poincaré.)
In April 1829, on the recommendation of Louis Richard,
Galois published his first paper
(Proof of a Theorem on Periodic Continued
Fractions) in the Annales de
Gergonne.
On May 25 and June 1, 1829, he submitted to the Academy his early research
on equations of prime degree
(such an equation is solvable by radicals if and only if
all its roots are rational functions of any two of them). He was 17.
Tragedy struck on July 2, 1829 when his father hanged himself in
an apartment located close to Louis-le-Grand. The elder
Nicolas Gabriel Galois (1775-1829) was an ardent republican
who had been elected mayor of Bourg-la-Reine in 1815
(where a street now bears his name).
His nemesis, the new right-wing priest of Bourg-la-Reine,
had managed to frame him by forging his
signature on malicious epigrams directed at Council members.
The ensuing scandal was more than what Mayor Galois could take.
His suicide sent the young Galois in a tailspin.
The new priest officiated at the burial
of the beloved Mayor, which turned into a riot...
(That priest wasn't
a Jesuit, in spite of what's often reported.)
Evariste was scheduled to take the Polytechnique entrance exam later that
month for the second and last time. Of course, he failed.
Louis Richard then insisted that he should attend Normale.
So, all was not lost...
Evariste Galois befriended fellow republican Ernest Duchâtelet
(Ernest-Joachim Armynot du Châtelet, born 19 may 1812 to a famous
noble family)
an effeminate law student at the time,
he would later become a student at the Ecole des Chartes, a learned journalist,
an absinthe alcoholic and a constant companion to one Louis-Achille Boblet
(most notorious for collecting coins rescued from the Seine River).
Duchâtelet had also just lost his father (1829) and his mother
had passed away years earlier (1820).
Normal Subgroups
|
Galois Rings.
|
Galois Fields
"Galois, le mathématicien maudit" by
Norbert Verdier (Belin, 2011).
French dueling pistols gunsmiths (c. 1830) :
Nicolas-Noël Boutet (1761-1833)
Le Page
|
Gastinne-Renette
|
Le Faucheux
Les
condisciples de Galois en Maths spé by Olivier Courcelle (2016-08-09)
| | 
Yvon-Villarceau, 1883
(by Eugène Pirou)
|
Antoine Yvon Villarceau (1813-1883)
Serge Mehl (French)
|
Villarceau circles
|
Wikipedia
&
Wikipédia
Born Antoine François Joseph Yvon, he later transformed his last name
to Yvon Villarceau (which he spelled without an hyphen).
Villarceau was the name of a land he once owned and
bequeathed to the town of Vendôme.
He became known simply as Villarceau
(this avoids the confusion brought about by the fact that Yvon
is a popular first name, but it wasn't his).
Villarceau graduated from
Ecole
Centrale (1840). He is best remembered for discovering or rediscovering, in 1848,
an amazing elementary fact:
The intersection of a torus with a doubly-tangent plane consists
of two intersecting circles (Villarceau circles).
He was a member of the French Académie des sciences.
"Théorème sur le tore", M. Yvon Villarceau
Nouvelles Annales de mathématiques, 7, pp. 345-347 (Paris, 1848)


Pierre Alphonse Laurent (1813-1854; X1830)

MacTutor
|
Wikipedia
&
Wikipédia
Pierre Laurent was married (in Haumont, on 1841-10-18) to
Palmyre Angélique Bernardine Depreux (b.1821).
They had three children.
Their son, Pierre Georges Laurent (b.1843) also
became a Polytechnicien (X1861).
Laurent polynomial
|
Doubly infinite Laurent series (1848)
Auguste Miquel (1816-1851)
Serge Mehl (French)
|
Jean-Louis Aymé (2012-10-30)
|
Wikipédia
He was born in Albi in 1816.
He graduated from high-school in Toulouse,
first as bachelier ès lettres (1834)
then bachelier ès sciences (1835).
Auguste Miquel then went to Paris to prepare for the Grandes Ecoles
entrance competition. He attended
Saint-Louis
and was also coached privately at Institution Barbet,
where he proved to be extremely brilliant.
Located 3, impasse des Feuillantines (Paris V)
from 1827 to 1864, the Institution Barbet was
one of several competing private preparatory schools
(other examples include
Collège Rollin and
Institution Mayer).
The founder of this particular institution of higher learning was
Jean-François Barbet (1799-1880)
who was one of only four students who entered the scientific section
of the Ecole Normale in 1820.
The other three were: François Artaud
(possibly the son of
Alexis-François
Artaud de Montor, 1772-1849),
the geometer Georges Ritt (1800-1864) author of several textbooks, and
Roch Roustan (1801-1870) future recteur of
Aix.
The Barbet boarders were auditing the Mathématiques
Spéciales lectures given at Saint-Louis,
by either Delisle or Vincent.
Known to his students as "père Pancu" (because he'd mispronounce
"perpanculaire" instead of perpendiculaire)
Augustin Delisle [Delille] had been appointed
"agrégé en mathématiques au collège royal de Henri IV"
in 1817, before agrégation became a formal competition (1821).
He taught at Saint-Louis until his retirement in 1852
(he died in June 1881).
On the other hand,
Alexandre-Joseph Vincent
(1797-1868) was a former student of Ecole Normale (1816) who had originally been
appointed "agrégé en physique à Reims", in 1820.
In 1836, while still a student at Barbet, Auguste Miquel proved
several clever theorems about intersecting circles.
At that critical stage of his curriculum,
such specialized research may have taken too much of a toll:
Miquel didn't make the cut for Polytechnique or
Ecole Normale.
Shortly thereafter, he would start earning a living as a high-school teacher,
with the lowly rank of régent,
without ever becoming an agrégé
or obtaining a doctorate.
Miquel was a staunch republican.
He published his anti-royalist views in social-democratic journals.
In those days, that didn't do much good for his humble career, which
can be summarized as follows (from scattered nomination records):
- -1838 : Régent de mathématiques,
Collège de Nantua.
- 1838-1840 : Régent de mathématiques,
Collège de Saint-Dié.
- -1842 : Régent de mathématiques élémentaires,
Collège de Castres.
- 1842- : Régent de mathématiques, Collège de
Bagnols.
- 1842-11-09 : Granted a one-year sabbatical.
- -1846 : Professeur, Collège de Castres.
- -1849 : Régent de mathématiques,
Collège du Vigan.
- 1849- : "... appelé à d'autres fonctions."
NOTE: In the same period, an unrelated "Miquel" held positions in primary education at
Seyne (1840) Barcelonnette (1841) and Toulon (1843-1855).
Miquel called syntrepent curves
two planar curves which rotate about two fixed points as they roll on each other without slipping.
He coined the word isotrepent
for a curve syntrepent to itself (the ellipse is a great example).
Auguste Miquel's first scientific publication appeared in 1836
on page 486
of the short-lived monthly journal
Le Géomètre,
founded that same year by the liberal activist Antoine-Philippe Guillard
(1795-1870) a former student at Ecole Normale (1813)
who had been appointed
"agrégé de mathématiques au collège royal de Louis-le-Grand", in 1819.
Miquel's subsequent work was mostly published in
Joseph Liouville's
Journal
de mathématiques pures et appliquées (founded in 1836) including:
-
"Sur quelques questions relatives à la théorie des courbes",
Journal de mathématiques pures et appliquées,
III, pp. 202-208 (1838).
-
"Théorèmes de Géometrie",
JMPA, III, pp. 485-487 (1838).
-
"Théorèmes
sur les intersections des cercles et des sphères",
Journal de mathématiques pures et appliquées,
III, pp. 517-522 (1838).
-
"Mémoire de Géometrie",
JMPA, IX, pp. 20-27 (1844).
-
"Mémoire de Géometrie (deuxième partie)",
JMPA, X, pp. 347-350 (1845).
-
"Mémoire de Géometrie (troisième partie)",
JMPA, XI, pp. 65-75 (1846).
He also used the
pedagogical
counterpart (1842-1927) of Liouville's journal:
-
"Problème d'Optique",
Nouvelles annales de mathématiques, 5, pp. 235-238 (Paris, 1846).
Auguste Miquel died in 1851, at age 35, in obscure circumstances.
Enseigner les
mathématiques au XIXème siècle
|
Miquel point
|
Miquel's pentagram
|
Miquel's Theorem (Dutch)


Victor Alexandre Puiseux (1820-1883)
Ph.D 1841
|
MacTutor
|
Academic career (French)
|
Weisstein
|
Wikipedia
Victor Puiseux was born in Argenteuil
(where a lycée and a street now bear his name) but
his family relocated to Lorraine
when he was three years old.
Victor received his secondary education at the Collège de
Pont-à-Mousson.
Upon graduation from high-school (1834) Puiseux was awarded a scholarship to attend
Collège Rollin, a top-notch Parisian preparatory school
where Charles Sturm (1803-1855)
was still professeur de mathématiques spéciales (1830-1838).
Rollin students also attended lectures in
lycée Louis-le-Grand.
Puiseux entered Ecole Normale Supérieure in 1837
and obtained his agrégation in 1840 (ranking first nationally,
ahead of his older classmate Charles Toussaint, 1817-1892).
That stellar performance earned Puiseux a position of chargé de conférence
at Ecole Normale in Paris for one year (1840-1841). That gave him enough free time
to prepare for a doctorate, which he duly obtained on
1841-08-21,
at the ripe old age of 21, with two reportedly uninspired theses (23 pages total) entitled:
1. Sur l'invariabilité des grands axes des orbites des planètes.
[Updated in 1878.]
2. Sur l'intégration des équations du mouvement d'un système de points matériels.
Puiseux was then nominated (1841)
professeur de mathématiques élémentaires au collège royal de Rennes.
where he was promoted professeur de mathématiques spéciales
the next year (1842-11-14) thus succeeding Etienne Bigourdan
who went on to a similar position in Rouen.
The job Puiseux thus left in 1842 was given to one Mr. Thiébault,
coming from Bourges.
In 1844, Puiseux (possibly foregoing an offer of a University position)
would be officially ordered to hold on to
his position in Rennes, because his own suppléant (Mr. Paignon, agrégé in 1844)
would himself be called upon to teach in mathématiques élémentaires
for the duration of a leave of absence (1 year) then granted to the aforementioned Thiébault.
Victor Puiseux then became professor of pure mathematics at the
University of Besançon
for two years (1845-1847). Elected secretary of the Faculty in 1847.
The occupation of Victor Puiseux in 1848 is unknown to this writer at this time.
In 1849, Puiseux went back to Paris as a maître de conférence
in Ecole Normale, replacing
Jean-Marie Duhamel
(1797-1872; X1814). He would hold this position until 1855.
Simultaneously (in 1853), he was appointed to the Collège de France
as suppléant of
Jacques Binet (1786-1856; X1804)
in the chair of astronomy.
In 1856, Victor Puiseux is chargé de cours at
the Sorbonne
and soon succeeds Augustin Cauchy (1789-1857)
as professor of mathematical astronomy and celestial mechanics.
He held that chair for 26 years (1857-1883) until his death.
Puiseux was the doctoral advisor of Camille Jordan (1860).
On 1878-01-18, his only other doctoral student
(Spiru Haret, 1851-1912)
defended a thesis bearing the exact title Puiseux himself
had used for his own doctoral work, 36 years earlier, namely:
Sur l'invariabilité des grands axes des orbites des planètes.
What Haret established in his doctoral work, using third-order pertunation methods,
was that the principal axes of planetary orbits undergo secular variations, which would seem to
make them unstable in the long run. That surprising result was an inspiration for the
chaos theory of
Henri Poincaré.
It was also the motivation for later work (1954) by
Kolmogorov who was almost able claim the
absolute stability of the Solar system for deeper reasons.
Simultaneously, Puiseux served as
maître de conférence from 1862 to 1868
at Ecole Normale, where he taught
probabilities and
differential calculus.
He held a post at the
Bureau des Longitudes
(in the bureau des calculs service) from 1868 to 1872.
He was elected, by a unanimous vote, to the geometry section of the
Académie des sciences on 1871-07-10.
Victor Puiseux also rose to the administrative rank of
inspecteur général de l'Instruction publique, hors cadre.
As such, in 1880, he was put in charge of inspecting "all primary schools educating holders of State scholarships".
This strange parlance was the way all public elementary schools were called, just
before the momentous 1881 reforms famously instigated by
Jules Ferry (prior to which,
all families who could afford it were paying full tuition to educate their children, even in the public system).
Puiseux died at the age of 73, on 9 September 1883, in
Frontenay, the village of the family of
his new daughter-in-law, shortly after her wedding (1883-06-21) to his eldest son, Pierre.
He had requested that no speech should be made over his dead body.
He had six children but was survived by only two sons, both of them astronomers:
Pierre Puiseux (1855-1928) and
André Paul Puiseux (1858-1931).
Puiseux series 1850
(Newton, 1676)
|
Bertrand-Diquet-Puiseux theorem
|
J. Dieudonné on
Algebraic Geometry


Guillaume Jules Hoüel (1823-1886)
MacTutor
|
Wikipedia
Jules Hoüel was born on April 7, 1823 in the small town
of Thaon (10 km NW of Caen,
spelled "Than" before 1843, which is the way the name is still pronounced).
He was educated at the Lycée Royal de Caen and at the
Collège Rollin in Paris, which housed one of the top preparatory schools.
The private
Collège
Rollin took that name in 1830.
It had been founded in 1821 by Joseph Planche and l'abbé Charles Nicolle (1758-1835)
as a "new" Collège Sainte-Barbe and was once
called Sainte-Barbe Nicolle or
Sainte-Barbe Rollin to distinguish it from the older
Sainte-Barbe
revived by Victor de Lanneau (1758-1830)
in 1798 on Montagne Sainte-Geneviève
The latter, which lasted until 1999, was built on the same land as the historical
Collège Sainte-Barbe founded in 1460,
which gave it a much stronger claim to the prestigious historical name,
as was legally recognized in 1830.
Sainte-Barbe (Barbara)
being the patron saint of miners, engineers, architects
and mathematicians is also the patron saint of Polytechnique, which explains the
great symbolic prestige of her name for a French preparatory school.
In 1876, Rollin would move from its original location (rue Lhomond)
to its current address (avenue Trudaine).
It lost its private status and was taken over by the municipality,
becoming Lycée Rollin in 1919.
The school was renamed in 1944 after the communist resistance fighter
Jacques Decour (1910-1942)
who had started teaching there in 1937, under his real name of Daniel Decourdemanche.
Hoüel became normalien in 1843
and agrégé in
1847
(7 out of 9 that year).
He first taught in the lycées of
Bourges, Bordeaux, Pau and Alençon (1851).
On 1855-08-18,
he obtained a doctorate for a thesis in celestial mechanics which
impressed Urbain Le Verrier who offered him to
join the Observatoire de Paris.
Hoüel turned down that offer.
Instead, he spent a couple of years on independent
mathematical research at his family home in Thaon.
He was appointed professor of
Mathématiques spéciales at Caen for just
a few weeks (January-March 1856) to replace
Charles Toussaint who became censeur
of the lycée at that time.
In March, Antoine-Xavier Planes took over. Toussaint got his old job back in October.
In 1858, Hoüel was appointed to the chair of pure mathematics in
Bordeaux,
which he held until he retired (1884).
He had a passion for non-Euclidean geometry and a gift for languages:
In 1866, he learned Russian to translate
Lobatchevsky
and Hungarian to read Bolyai...
In his translation of their work (1870) Houël published a proof of
Beltrami (1868) which marks the high point of the subject.
With the younger
Gaston Darboux (1842-1917) Jules Hoüel became founding editor of
Bulletin des sciences mathématiques et astronomiques in 1870.
Blog à Maths
|
Norbert Verdier
|
François
Plantade

Théophile Pépin (1826-1904) older brother ?? of...
Jean François Pépin (1829-??; X1849)
Wikipedia

Pépin's counterexamples to the Hasse principle for curves of genus 1.
Pépin's test


Louis Paul Cailletet (1832-1913)
Genealogy
&
Bio (French)
|
Britannica
|
Wikipedia
Born on 21 September 1832 in Châtillon-sur-Seine
(Côtes d'Or; Eastern France).
He was educated at Lycée Henry LV in Paris.
He attended cole des mines de Paris in 1852-1853,
with his brother
Camille (1834-1860).
Paul Cailletet was the first person to liquefy oxygen (1877-12-02) using
the Joule-Thomson effect for which he received the
Davy Medal in 1878, with
the Swiss physicist Raoul Pictet (1846-1929)
who reported the same feat by different means on 1877-12-22.

Emile Léonard Mathieu (1835-1890; X1854)
MacTutor
|
Wikipedia
|
Mathieu functions
|
Mathieu groups
|
Mathieu transform
Born on 5 May 1835 to Nicolas Mathieu, caissier à la recette générale
and his wife Amélie Antoinette Aubertin.
He passed away on 19 October 1890 (aged 55) in Nancy
where he had been holding a chair of mathematics since 1873.
He received his doctorate (Docteur ès Sciences)
in 1859 for a thesis on transitive functions which would lead him to the
discovery (between 1860 and 1873) of the five
sporadic simple groups now named after him.
The personal address he gave when he entered Polytechnique (1854)
was 12 rue Chevremont (Metz, Moselle).
Emile Mathieu had been ranked 168 on the entrance exam and
was 152 out of 158 students passing into the second year.
His French military records give of him the following physical description:
Cheveux châtains - Front moyen - Nez moyen - Yeux roux - Bouche large - Menton rond - Visage ovale - Taille 166
- Un signe particulier à la joue droite.
No extant portrait known.
Unrelated individuals named Emile Mathieu include:
Ambitions parisiennes contrariées
|
No known portrait


Gustav Adolph Roch (1839-1866)
Ph.D. 1862
|
MacTutor
|
Wikipedia
|
Halle (German)
On the advice of his father (an assistant cook)
Gustav Roch went to the Polytechnic Institute in his hometown of Dresden
(Technische Bildungsanstalt) to train for a career in chemistry.
One teacher there was
Oscar
Schlömlich (1823-1901) who had studied at Berlin under
Dirichlet and Steiner.
Schlömlich noticed the mathematical abilities of Roch and persuaded
him to switch his major to mathematics and physics.
To accomplish this effectively, Roch had to take remedial courses at a private institution outside
of the Polytechnic Institute.
In 1859, Roch published his first paper in
Schlömilch's Zeitschrift für Mathematik und Physik
(a journal founded by Schlömilch three years earlier).
In the Spring of 1859, Gustav Roch entered the University of Leipzig.
Riemann-Roch theorem
(Riemann 1857, Roch 1865)

François Edouard Anatole Lucas (1842-1891)
MacTutor
|
Wikipedia
|
Anne-Marie Décaillot
(1999)
|
Roland Brasseur (2014)
Edouard Lucas is the most prominent French number-theorist of
the nineteenth century.
As number theory
wasn't fashionable in French Academia,
Lucas made a living outside of his specialty.
He was born in Amiens (where a College and a street now bear his name)
to a family of modest means.
Of his 10 siblings, 2 were stillborn and 2 died young.
Edouard was a brilliant student and would always be supported by scholarships.
After graduating from high-school in Amiens (1859), Edouard Lucas attended
mathématiques spéciales for two years at the
lycée impérial de Douai,
first under Claude David (1811-1864)
then under Louis Painvin (1826-1875).
On his second try, Lucas became a
normalien
in Paris (1861).
He got his agrégation in
1864, outranked only by
Gaston Darboux (1842-1917).
Because he was not yet 25, his official nomination as
agrégé was delayed.
Lucas was an associate astronomer at the Paris Observatory from 1864 to 1869, in the midst of
a long period of bitter tensions (1854-1870) between the scientific staff and the director
Urbain le Verrier (1811-1877; X1831)
the discoverer of Neptune (1846-08-31).
Starting in 1867, Lucas would escape from Le Verrier's constant
mobbing
by studying mathematical problems in his hometown of Amiens.
He became acquainted with the mathematics pertaining to
the industrial weaving of fabrics (using
Jacquard punchcards)
through the work of another native of Amiens:
Edouard Gand (1815-1891) who had founded the
Société industrielle d'Amiens in 1861.
This would provide the topic of Lucas' first publication (1867).
Lucas was sacked by Le Verrier in the Summer of 1869 and appointed to teach
high-school seniors in Tours, with a decrease in pay (1869-09-08).
His refusal of the position left him with only a low allocation and he joined
the army as a junior officer.
He served as a decorated artillery officer in the
Franco-Prussian War (1870-1871)
and rose to the rank of captain.
On 1872-04-10, he was nominated professor of
mathématiques spéciales in the small town of
Moulins, where he stayed
until he was offered more desirable positions in Paris, alternating between
Lycée Charlemagne
(1876-1879, 1890-1891) and
lycée Saint-Louis
(1879-1890). He was granted an extended leave of absence from Saint-Louis for two
school years (1882 to 1884) after the death of his wife of 9 years
(Marthe Boyron, 1852-1882, mother of his two children).
During that time, he prepared an edition of the works of Fermat.
His last transfer from Saint-Louis to Charlemagne (1890-08-20)
was actually a switch of equivalent positions between himself and
Gaston Gohierre de Longchamps (1842-1906).
Several students of Saint-Louis had threatened to leave the school if they were assigned to
the class of Lucas, because they thought that his style would not prepare
them adequately for the competition they were facing.
Apparently, Lucas did not face the same (unfounded) rejection at Charlemagne,
where he ended up spending the last year of his life.
Lucas died at the age of 49 (3 October 1891)
from a severe infection following a freak accident:
A waiter had wounded his cheek with a broken plate at a banquet of the
Association française pour l'avancement des sciences
(AFAS).
Edouard Lucas is buried in Montmartre Cemetery.
In 1876, Lucas proved the primality of a 39-digit number
(the 12th
Mersenne prime) which would remain
the largest known prime for 75 years (until 1951):
2127 - 1 =
170141183460469231731687303715884105727
To do so, over the course of 19 years (he had started to work on the problem at age 15)
Lucas eventually devised a specialized primality test for Mersenne numbers
(i.e., numbers which come just before a power of two).
That test was streamlined in 1930 by
Derrick H. Lehmer
(1905-1991) as part of his own
doctoral dissertation
at Brown University.
The Lucas-Lehmer test
remains, to this day, the most efficient way
to prove the primality of some large numbers.
The most prominent publication of Edouard Lucas on
Number Theory is:
Théorie des nombres
528 pages (Gauthier-Villars, Paris, 1891)
Lucas polynomials (1878)
|
Towers of Hanoi (1883)
|
Umbral calculus
|
Lucas pseudoprimes
 
Jules Tannery (1848-1910)
MacTutor
|
Wikipedia
|
Dico Spé
|
Career
Like his older brother
Paul
Tannery (1843-1904), Jules Tannery was an alumnus of the
"Taupe Laplace"
(Lycée Malherbe de Caen) where he taught briefly (1871-1872) early in his career.
His star student at the time was
Léon
Lecornu (1854-1940) who later became a member of the
Académie des sciences.
Tannery earned his doctorate in 1874
at the Ecole Normale Supérieure (ENS) under
Charles Hermite (1822-1901; X1842)
[the man who had proved the transcendentality of e
just one year earlier, in 1873].
Jules Tannery was first appointed at ENS-Ulm in 1881 and also took up lecturing duties at
ENS-Sèvres in 1882, shortly
after its creation (that counterpart of ENS-Ulm for girls had been
created in 1881 and fused with ENS-Ulm in 1985).
Tannery supervised four doctoral students, including
Jacques Hadamard (1865-1963,
who proved the Prime
Number Theorem) and Jules Drach (1871-1949).

Other students of Tannery's at ENS included the likes of
Paul
Painlevé (twice a Prime Minister of France, in 1917 and 1925)
and
Émile Borel (1871-1956).
Jules Tannery was elected to the French
Académie des sciences in 1907.
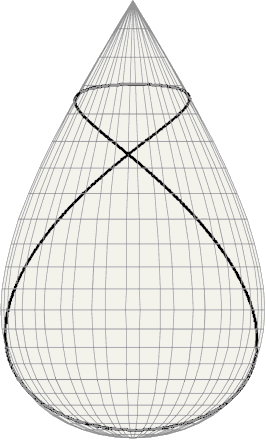
Tannery devised the teardrop-shaped surface of revolution pictured at left,
dubbed Tannery's pear, as
a single lobe of the two-lobe algebraic surface
(degree 4) of cartesian equation:
8 a2 (x2 + y2 )
=
(a2 - z2 ) z2
Parametrically, for both lobes:
x =
(a / Ö32) sin u cos v
y =
(a / Ö32) sin u sin v
z =
a sin u/2
Every geodesic curve (like the bold line shown at left)
is an algebraic
closed curve
that goes around the axis twice and crosses itself once!
If need be, the entire surface described by the above
unrestricted equations can be called Tannery's hourglass
(it consists of two distinct congruent Tannery pears
sharing the same axis and the same cone-point ).
The cone's half-angle is:
Arctg 1/Ö8 = 19.47122...°
Jules Tannery is also remembered for
Tannery's Limiting Theorem
which states that the limit of an infinite sum is the sum of the limits, under
certain conditions...
Mathematical Genealogy
|
Teaching Geometry
|
Tannery's Limiting Theorem
 
François Proth (1852-1879)
The Prime Pages
|
Wikipedia
|
Up Closed
Proth was a promising self-taught French mathematician who made a living as a farmer.
He died young. The circumstances of his death are unknown.
Biographical details about him are scarce. He published 4 papers on number theory.
He is best known for Proth's theorem (1878)
which provides an efficient primality test
for integers of the form k . 2n + 1
with k < 2n (Proth numbers).
In 1878, eighty years before Norman L. Gilbreath, Proth formulated what's best known
as the Proth-Gilbreath conjecture.
Originally a simple doodle, that conjecture is ultimately a statement about the
distribution of the primes (Proth gave an erroneous proof in 1878).
| 2 | | 3 | | 5 | | 7 | | 11 | | 13 | | 17 | |
19 | | 23 | | 29 | | 31 | | 37 | | 41 | | 43 | |
47 | | 53 | | 59 | | 61 | | 67 | | 71 | | 73 | |
79 | | 83 |
| 1 | | 2 | | 2 | | 4 | | 2 | | 4 | | 2 | |
4 | | 6 | | 2 | | 6 | | 4 | | 2 | | 4 | |
6 | | 6 | | 2 | | 6 | | 4 | | 2 | | 6 | |
4 | | 6 |
| 1 | | 0 | | 2 | | 2 | | 2 | | 2 | | 2 | |
2 | | 4 | | 4 | | 2 | | 2 | | 2 | | 2 | |
0 | | 4 | | 4 | | 2 | | 2 | | 4 | | 2 | |
2 |
| 1 | | 2 | | 0 | | 0 | | 0 | | 0 | | 0 | |
2 | | 0 | | 2 | | 0 | | 0 | | 0 | | 2 | |
4 | | 0 | | 2 | | 0 | | 2 | | 2 | | 0 | |
0 |
| 1 | | 2 | | 0 | | 0 | | 0 | | 0 | | 2 | |
2 | | 2 | | 2 | | 0 | | 0 | | 2 | | 2 | |
4 | | 2 | | 2 | | 2 | | 0 | | 2 | | 0 |
| 1 | | 2 | | 0 | | 0 | | 0 | | 2 | | 0 | |
0 | | 0 | | 2 | | 0 | | 2 | | 0 | | 2 | |
2 | | 0 | | 0 | | 2 | | 2 | | 2 | | 2 |
| 1 | | 2 | | 0 | | 0 | | 2 | | 2 | | 0 | |
0 | | 2 | | 2 | | 2 | | 2 | | 2 | | 0 | |
2 | | 0 | | 2 | | 0 | | 0 | | 0 |
| 1 | | 2 | | 0 | | 2 | | 0 | | 2 | | 0 | |
2 | | 0 | | 0 | | 0 | | 0 | | 2 | | 2 | |
2 | | 2 | | 2 | | 0 | | 0 | | 0 |
| 1 | | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
2 | | 0 | | 0 | | 0 | | 2 | | 0 | | 0 | |
0 | | 0 | | 2 | | 0 | | 0 |
| 1 | | 0 | | 0 | | 0 | | 0 | | 0 | | 0 | |
2 | | 0 | | 0 | | 2 | | 2 | | 0 | | 0 | |
0 | | 2 | | 2 | | 0 | | 0 |
| 1 | | 0 | | 0 | | 0 | | 0 | | 0 | | 2 | |
2 | | 0 | | 2 | | 0 | | 2 | | 0 | | 0 | |
2 | | 0 | | 2 | | 0 |
| 1 | | 0 | | 0 | | 0 | | 0 | | 2 | | 0 | |
2 | | 2 | | 2 | | 2 | | 2 | | 0 | | 2 | |
2 | | 2 | | 2 | | 0 |
| 1 | | 0 | | 0 | | 0 | | 2 | | 2 | | 2 | |
0 | | 0 | | 0 | | 0 | | 2 | | 2 | | 0 | |
0 | | 0 | | 2 |
François Proth was a farmer in the small village of
Vaux-devant-Damloup
(near Verdun, France) where
the famous Fort de Vaux is located.
The village would be completely destroyed during the
Battle of Verdun,
the longest battle of WWI. It has now been rebuilt, 500 m downhill.
That's the only such revival in the infamous red zone
of the Verdun battlefield (72 inhabitants in 2014).
Proth numbers
|
Proth primes
|
Proth's theorem
|
Pocklington primality test
|
Gilbreath's conjecture (Proth, 1878. Gilbreath, 1958.)



François Cosserat (1852-1914; X1870)
MacTutor
 Lucien Cosserat (1856-1897; X1875)
Lucien Cosserat (1856-1897; X1875)
Eugène Maurice Pierre Cosserat
(1866-1931; ENS 1883)
MacTutor
|
Wikipedia
Lucien Constant Cosserat contributed to the joint work of his two brothers.
However, due to his early demise, he couldn't co-sign the masterpiece
on micropolar elasticity published by François and Eugène in 1909.
Genealogy :
The father of the three brothers was
François-Constant Cosserat, a well-off entrepreneur based in Amiens, France.
He was granted a British patent (number 1798) for improvements in
industrial smoke-burning furnaces on July 18, 1864.
Mathematical Genealogy
|
Correlator
"Théorie des corps déformables" by Eugène & François Cosserat
(Hermann, 1909). 230 pages.
 
Paul Emile Petit (1862-1936)
Officier de la Légion d'Honneur
|
Founder of the
Mines
de Nancy school
Paul Petit was born on 29 March 1862 in Lucy, Meurthe.
He entered the Ecole Normale Supérieure (ENS, Ulm)
in 1883 (placing last; 20/20).
Before graduation, he was appointed professeur de physique in a newly-created
position at Collège de Barbezieux (1886-02-13) future Lycée Elie Vinet.
Petit duly graduated from ENS in 1886 with an Agrégation in physics
(again, taking the very last slot; 9/9).
In 1886, he became sous-directeur in the Laboratoire des Hautes-Etudes
created by Berthelot.
In March 1889, Petit obtained a doctorate in chemistry.
Thereafter, he spent his entire career in Nancy, where he was first appointed
chargé de cours in chemistry on 1889-10-31.
In 1893, Petit founded the
Ecole de Brasserie de l'Université de Nancy, of which he was the first administrator.
In 1894, he was appointed Professeur de Chimie Agricole.
He later rose to the rank of Doyen de la Faculté des Sciences de Nancy.
On 28 March 1919, Paul Petit was instrumental in the creation of the
Institut Métallurgique et Minier de Nancy, a major engineering school which everybody would soon call
Les Mines de Nancy. The official name changed several times. Since 1985, it is:
Ecole Nationale Supérieure des Mines de Nancy.
Paul Petit was its first academic director in 1919 (when it was part of the University of Nancy).
Ecole
des Mines de Nancy (1919-2009)
 
Henri Eugène Padé (1863-1953)
MacTutor
|
Wikipedia
|
"Asymptotology"
by Igor V. Andrianov & Leonid I. Manevitch
Henri Padé was born on 1863-12-17 in
Abbeville
to a family hailing from the nearby rural village of
Cahon
(250 inhabitants; modern French postal code 80132).
His father, Jean-Baptiste Domice Padé,
was a rouennier
(see below) born in Cahon
on 1821-02-15, the son of a shepherd born in 1790 and the grandson of a weaver born in 1765.
Henri's mother, Joséphine Pétronille Eléonore Thiébault
was born in Cahon on 1831-09-27. She was the daughter of a weaver born in 1794.
Jean-Baptiste and herself were married in Cahon on 1859-02-25.


Rouenneries are cotton fabrics in which threads were dyed
in various shades of red before weaving. Such threads were
first spun in 1787, on state-owned spinning machines operating in
Rouen (hence the name).
Weaving was mostly done in the
Pays de Caux
around Yvetot.
That was the fashion for over 60 years, from
the First French Empire onward.
In 1863, about 60,000 looms were in operation
in the Pays de Caux and another 20,000 were located in nearby
Picardy, where Cahon is.
People who worked the fields in summertime would work the looms in the Winter.
A loom was attended by one weaver and one assistant (who was often a woman or a child).
This occupation was more highly regarded than agriculture and those who did both
called themselves weavers (tisserands).
On Henri's birth certificate, Jean-Baptiste Padé said he was
marchand de rouenneries,
implying he would mostly trade or sell the merchandise, rather than weave it himself
(unlike a tisserand, employed by a fabricant).
Shortly after Henri's birth, the shortage of cotton brought about by the
American Civil War (1861-1865)
precipitated the downfall of this rural activity, which was subsequenly mechanized
on an industrial scale,
in Amiens and elsewhere.
Henri Padé
completed his secondary education in Lille at the age of 17
(his baccalaureate was officially awarded on 1881-09-30).
He then underwent two years of preparatory school at
Lycée Saint-Louis.
Padé entered the prestigious
Ecole
Normale Supérieure in 1883, tenth of a list of 20,
given below in order of merit.
The first 11 were nominated on 1883-08-07
in a list of 20. Of those, 9 chose Polytechnique and were replaced by a list of 9
published on 1883-10-19.
Only the next-to-last on that second list (Pierre Labarbe) chose Polytechnique and
he was replaced by Paul Petit on 1883-10-27.
Unexplicably, the 1884 summary of the results below showed only 19 names.
Paul Franc was omitted
(although his misspelled name is still in the current records of the ENS).
My guess is that he passed away in 1883 or 1884.
The only other trace of Paul Léon Félix Franc I could find is from
Recueil des lois et actes de l'instruction publique (1883, p. 652)
which says that he won a Prix d'honneur (1883-08-06) in the
Concours Général
for students competing outside Paris & Versailles,
as a mathématiques apéciales student at
the Lycée de Nancy under
Alphonse Hervieux
(1846-1906, ENS 1867).
- Jules Riemann (1863-1941). Professor at Louis-le-Grand. Cor's
co-author.
- Paul [André Marie] Janet
(1863-1937).
Agrégé in Physics (1/9) in 1886.
- André [Grégoire] Duboin. First prize in chemistry
CG. Louis-le-Grand.
- Félix [Guillaume Joseph] Bonnel. On a scholarship from Lyons (1881).
- Eugène Cosserat (1866-1931). The youngest of the Cosserat Brothers.
- [Théodule] Edmond Colléatte
(1864-fl.1933). Agrégé in Physics (4) 1893.
- Paul [Léon, Félix] Franc. Prix d'honneur en maths spé (Nancy, 1883).
- Maurice Lelieuvre (1864-1949). Successor of Cor
at La Taupe Laplace.
- Narcisse Cor (1863-1949) who got a coveted scholarship to Göttingen.
- Henri Padé (1863-1953). Studied Padé approximants from 1891 to 1907.
- Paul Painlevé (1863-1933).
Mathematician & statesman (prime minister).
- [Julien] Octave Rouen
- Emile [Henri, Jean-Baptiste] Chrétien
(1861-1955). Professeur de Lycée.
- Charles Roos
- [Pierre] Raymond Le Vavasseur (1862-1930). Group theory.
- [Pierre] André Puzin (1861-). Agrégé in Mathematics in 1887 (12/13).
- Lucien Poincaré (1862-1920).
Brother of Raymond, cousin of Henri.
- Louis Régis (1866-). Agrégé in Mathematics in 1887 (4/13).
- [Jules, Théaul] Albert Quiquet (1862-1934).
Leading actuary
& author.
- Paul [Emile] Petit (1862-1936). Founded Mines de Nancy school in 1919.
The star of that class, Jules Riemann, was ranked first overall upon admission and first in mathematics upon graduation (see below).
He doesn't seem to be directly related to Bernhard Riemann (1826-1866).
In physics, top honors went to Paul Janet, son of the French philosopher
Paul [Alexandre René] Janet (1823-1899).
At least three of the above (Cor, Painlevé and Padé) would go to Göttigen after graduation, to study under
Klein and Schwarz. Apparently, Padé had to take a longer route to do so (see below).
Henri Padé was awarded two licence degrees in August 1885 (Mathematics on the 15th,
Physics on the 20th). For ENS students, this was mostly a formality which served as insurance against the very real
possibility of failing the agrégation competition later
(back in those days, there were only 13 open slots per year in mathematics and 9 in physics).
In 1886, six " élèves sortants de l'ENS " got
their Agrégation de Mathématiques. Namely:
Jules Riemann (1) Eugène Cosserat (2) Narcisse Cor (5) Henri Padé (6)
Maurice Lelieuvre (7) and Paul Painlevé (9/13). Two made it in physics:
Paul Janet (1/9) and Paul Petit (9/9).
That wasn't the end of it, since you could compete any time after graduation.
Among those who entered ENS in 1883, two made it in mathematics on their second attempt
in 1887 (in a competition dominated by
Vessiot and Hadamard) namely:
Louis Régis (4) and André Puzin (12).
Likewise, Lucien Poincaré was successful in the physics contest of 1887 (6).
Two of their classmates had to wait a bit longer: Raymond Le Vavasseur got his agrégation
in 1889 (ranked 3rd, in Mathematics) and Colléatte was finally successful in 1893 (ranked 4th, in Physics).
All told, 13 of the 20 students who entered ENS in 1883 ended up agrégés
(9 in Mathematics, 4 in Physics).
At first, Padé was appointed professor of mathematics at the
lycée de Limoges
(which became lycée Gay-Lussac on 1889-02-09).
Henri Padé's nomination, dated 1886-09-04, was said to be temporary as was the custom for junior faculty.
He was indeed immediately reassigned to Carcassonne
instead (1886-10-21, still temporarily, of course).
The lycée de Carcassonne had been created in 1853 as an upgrade to the old collège communal
(it took the name of Lycée Paul Sabatier in 1960, when it moved from
its original location at 89, rue de Verdun).
Padé's next appointment was at Montpellier (1887-10-29)
in the Grand Lycée (of Medieval origin) which became the
Lycée Joffre when it moved in 1947.
At that time, Henri Padé published his first scientific paper, which dealt with the irrationality
of e and p (1888).
In 1889, he took a sabbatical from Montpellier to study in Germany.
He first spent one semester at Leipzig,
where he took the
course of Adolph Mayer
(1839-1908) on the differential equations of mechanics.
(He registered on 1889-10-18 and passed his final exam on 1890-03-28.)
Padé then transferred to
Göttingen where he stayed
for the entire year 1890-1891 (he was granted an unpaid leave of absence on 1890-12-03,
as a former professor at Montpellier).
On 1891-05-05, Padé obtained a degree in mathematics from Göttingen,
having attended lectures by Felix Klein (1849-1925) and
Hermann Schwarz (1843-1921).
At that time, he translated into French Felix Klein's celebrated
Erlangen Program (1872)
for the Annales de l'Ecole Normale Supérieure (1891).
Back to France, Padé undertook doctoral work under
Charles Hermite (1822-1901)
while resuming his teaching career with an appointment
at the Lycée de Poitiers (1891-09-19)
at a senior rank (2-ème classe)
contrasting with his previous nominations (6-ème classe).
A few months later (1891-12-11) he was appointed to the
Lycée de Lyon to teach a preparatory class for
Saint-Cyr.
On Friday 1892-04-08 at 14:00,
Henri Padé defended his doctoral thesis on the theory of what we now call
Padé approximants:
Sur la représentation approchée d'une fonction par des fractions rationelles.
Besides Hermite (thesis supervisor) the jury consisted of
Emile Picard (1856-1941) and
Paul Appell (1855-1930).
Padé passed avec toutes boules blanches (i.e., by unanimous vote).
His lesser thesis was entitled Formation des groupes fuchsiens. Fonctions modulaires.
Padé officially received his doctorate on 1892-06-21.
Also in 1892, he published a small educational book, prefaced by
Jules Tannery, entitled:
Premières leçons d'algèbre élémentaire, nombres positifs et négatifs,
opérations sur les polynômes (Gauthier-Villars & fils, Paris).
In 1893, he left his position in Lyons and was appointed (1893-09-02)
to a newly-created position near his hometown, teaching high-school seniors "A" at the
Lycée of Lille (which took its current name of
Lycée Faidherbe that very year).
In January 1897, Padé became Maître de conférences
at the nearby University of Lille,
succeeding Emile Borel (1871-1956)
who had been appointed to ENS in Paris. Padé taught rational mechanics
at IDN from 1897 to 1901,
putting to good use what he had learned from Adolph Mayer in Leipzig, 7 years earlier.
In 1901, Padé left Lille for Poitiers, as
chargé de cours.
In June 1902, he was promoted Professor of Rational and Applied Mechanics
at the University of Poitiers,
suceeding Antoine Henri Durrande (1831-1904; ENS 1851).
In November 1903, Henri Padé accepted an appointment as Professor of Mechanics
at the University of Bordeaux
(as re-founded on 10 July 1896) where he would become
Doyen de la Faculté des Sciences on 1906-12-07.
On 1906-12-17, Padé received the Grand Prix
of the French Academy of Sciences by winning a competition on
"better convergence criteria" for algebraic continued fractions.
His submission consisted of two sealed covers
(plis cachetés
filed in February and June 1903). This marked the peak of his research career.
Padé ended his career as a university professor on 1908-11-17, at age 44,
to become the youngest Rector
in France (there were 13 rectors at the time) successively heading the
Académies of
Besançon (November 1908)
Dijon (1917) and
Aix-Marseille (1923)
where he retired in 1934, at the age of 70.
Padé became a Knight of the Legion of Honor on 1910-05-06
(decorated by Appell)
and was promoted Officer of the Legion of Honor on 1927-03-09.
Henri Padé passed away in Aix-en-Provence
at the age of 89, on 1953-07-09.
He was survived by his wife of 60 years, Hélène Caudron,
whom he had married in Abbeville on 1893-08-12
(she was born on 1876-01-15, died on 1955-12-15 and is burried next to her husband).
Both Henri and Hélène Padé were good musicians.
He was fond of Schumann and Schubert. She played a grand piano.
They had three daughters. The eldest married before 1922.
The youngest, Odette, was the second wife of Georges Bonfils and the mother of Claude Bonfils.

Hélène & Henri Padé, at Beaucourt on 6 June 1922.
Between 1888 and 1907, Henri Padé wrote 42 scientific articles,
without any co-authors. 29 of his papers are about
continued fractions or Padé approximants.
A Brief History of Padé Approximants :
In 1730,
James Stirling (1692-1770) and
Daniel Bernoulli (1700-1782)
independently introduced Padé approximants.
Around the same time, Euler (1707-1783)
gave Padé-type approximations to the sums of some series.
In 1740, according to Claude Brezinsky (Birth and early developments of Padé approximants)
one George Anderson
stumbled upon three different rational approximations to the logarithm function.
Anderson was apparently a resident of Twickenham
who is only known through the eight mathematical letters he sent to
William Jones (1675-1749)
between 1736 and 1740
(at which time he said he was going to the University of Leyden,
the oldest university in the Netherlands).
In 1758, Johann Heinrich Lambert
(1728-1777) found some Padé approximants by direct computations of their coefficients.
In 1776, Lagrange (1736-1813)
obtained such approximations from the convergents of continued fractions.
In 1837, Kummer (1810-1893) used approximants as convergence accelerators.
In 1845, Jacobi (1804-1851) expressed
Padé approximants using determinants.
In 1861, Padé approximants appeared in the
doctoral thesis of
Hermann Hankel (1839-1873).
In 1870, the doctoral thesis of Frobenius (1849-1917) established
some relations between Padé approximants. Padé was surely unaware of this in 1892.
In 1873, Charles Hermite (Padé's
future thesis advisor) proved e to be transcendental
by using simultaneous Padé approximants of several series.
The methods introduced by Padé in his 97-page thesis (1892)
were used for divergent series
in the book which Emile Borel (1871-1956) published in 1901.
Padé approximants were given their modern name
by E.B. Van Vleck (1863-1943)
who also coined the locution Padé table in a 1903 paper.
At a meeting of the AMS
in Boston (1903) Van Vleck issued the following clarification:
The existence of approximants was, of course, well-known before Padé,
but no systematic examination of them had been made except by Frobenius,
who determined the important relations which normally exist between them.
Padé goes further, and arranges the approximants, expressed each in its lowest terms, into a table.
In 1948, the subject was resurrected for good by Hubert Stanley Wall (1902-1971) who had earned
his doctorate in 1927
from the University
of Wisconsin-Madison, with a thesis on that topic, under the aforementioned E.B. Van Vleck.
In 1987, a monograph of Adhemar Bultheel (c.1948-)
extended the scope of Padé approximants from one-sided formal power series to two-sided Laurent series.
Mathematical Genealogy
|
Padé tables
|
Continued fractions
|
Ellipse perimeter
 
Ernest Paulin Joseph Vessiot (1865-1952)
MacTutor
|
Dico Spé
|
L'œuvre scientifique
de M. Ernest Vessiot by Elie Cartan (1947)
In the 1884
entrance exam to the Ecole Normale Supérieure,
Vessiot was second only to Jacques
Hadamard (1865-1963) who was subsequently a classmate of his.
In the agrégation contest of
1887, he finished first and Hadamard second.
After his brilliant graduation,
Vessiot held several teaching positions, starting at Lyons in 1887,
then Lille (1892) Toulouse, Lyons again and Paris (1910).
Ernest Vessiot obtained his doctorate in 1892, under
C. Emile Picard
(1856-1941)
with a dissertation about the action of continuous groups of transformations
(Lie groups) on the independent solutions of a differential equation.
In that domain, he would later extend results of
Jules Drach (1902) and
Elie Cartan (1907).
In 1914, he succeeded
François Cosserat (1852-1914; X1870)
as president of the
Société Mathématique de France.
Vessiot would hold the post of director of the
Ecole Normale Supérieure
until his retirement in 1935.
Anong his few doctoral students:
Jacques Herbrand (1930) and
Marie-Louise Dubreil-Jacotin (1934).
He was elected to the Académie des Sciences in 1943.
Ph.D. 1892
|
Picard-Vessiot theory
|
Mathematical Genealogy
|
Correlator

Jules Joseph Drach (1871-1949)
MacTutor
|
Wikipedia &
Wikipédia
|
Work of Jules Drach
Jules Drach did his doctoral work at
Ecole Normale Supérieure under the supervision of
Jules Tannery
(just like Jacques Hadamard earlier).
Drach was chargé de cours at the University of Poitiers when
Henri Padé left for Bordeaux and he took over Padé's
duties. In 1904, he was officially appointed as the successor of Padé
in the chair of Mécanique rationnelle et appliquée.
Mathematical Genealogy
|
Rues de Ludres

André Gérardin (1879-1953)
Christian
Boyer (2005)
Born in Nancy. Died in Nancy.
Once described as "the most active mathematical descendant of
Edouard Lucas in France".
He is among the most quoted authors in the monumental
History of the Theory of Numbers (1919) by
L.E. Dickson (1874-1954).
Gérardin created and/or edited four periodical journals about Number Theory:
- Sphinx-Œdip (1906-1932...) monthly.
- Lettre Mathématique Circulante (1943-1944). No extant copies.
- Intermédiaire des Recherches Mathématiques (1944) with
Paul Belgodère.
- Diophante (Diophantus)
four times a year, from 1948 to 1952.
AFAS
|
Sur
quelques nouvelles machines algébriques
Paul Poulet
(1887-1946)
Poulet numbers
|
Super-Poulet numbers
|
ChronoMath (French)
|
Wikipedia
(French)
Paul Poulet was an autodidact Belgian mathematician best remembered for charting the
pseudoprimes to base 2
which he tabulated up to 50 million in 1926 and up to 100 million in 1938.
Those are now commonly
called Poulet numbers in his honor
(they're also known as Fermatians or Sarrus numbers ).
In 1918, Paul Poulet discovered the first
aliquot cycle
(where each number is the sum of the proper
divisors of its predecessor) namely:
( 12496, 14288, 15472, 14536, 14264 )
In 1925, Poulet published 43 new
multiperfect numbers,
including his discovery of the first two known 8-perfect numbers.
"Sur les nombres multiparfaits" by Paul Poulet,
49th conference of the Association française pour l'avancement des sciences (Grenoble, 1925)
"Tables des nombres composés inférieurs à 50 000 000
répondant au théorème de Fermat pour le module 2"
by Paul Poulet, 50th conference of the Association française pour l'avancement des sciences (Lyon, 1926)
"Tables des nombres composés vérifiant le théorème
de Fermat pour le module 2, jusqu'à 100 000 000"
by Paul Poulet, Sphinx (Brussels), 8, pp. 42-45 (1938).



Jacques André Bloch
(1893-1948; X1912)
MacTutor
|
Wikipedia
|
The
Mathematician in the Asylum of Charenton
Mathematics is a dangerous profession;
an appreciable proportion of us go mad.
John Edensor Littlewood (1885-1977)
Really? In about 500 world-class thinkers whose biographies were srutinized
to produce Numericana, only 15 have suffered serious mental disorders
at some points in their lives (often unrelated to stressful thinking):
Aitken,
Baire,
Boltzmann,
Cauchy,
Cavendish,
Eisenstein,
Gödel,
Grothendieck,
Heaviside,
Nash,
Newton,
Perelman,
Petryshyn,
Tesla and
Turing.
Just 3% of them (or 5%, to allow for underreporting).
If anything, that's less than the general prevalence...
Fortunately, very few go criminally insane,
the way André Bloch did just before turning 24.
Thereafter achieving mathematical productivity and ultimate serenity
alone in the corridor of a lunatic asylum, for the remaining 31 years of his life...
André Bloch was born on 20 November 1893, in
Besançon
(14, Grande Rue)
to Alfred Abraham Bloch (1855-1910) and his wife
Lucie Didisheim (1871-1912).
A year later, 13 November 1894, his brother Georges was born,
who had similar mathematical abilities
(Lucien Georges Bloch, 1894-1917; X1912).
Their mother, Lucie Didisheim, was from a wealthy family of Jewish watchmakers.
She was the daughter of Jacques Didisheim (1834-1889)
and his wife Fanny Juvenia Goldschmidt (1845-1917) after whom the
Juvenia
watchmaking house was called, which her husband created in 1860.
 There was also a slighty older sibling nicknamed Riquet :
Henry Bloch
(1891-1972) who married
Marcelle Marcita Henrieta Frankfurt
(1904-1993) and had four children,
including the literary critic Marie-Claude
de Brunhoff (1929-2007)
who was married for 39 years (1951-1990) to
Laurent de Brunhoff (1925-)
perpetuator of the Babar saga,
created in 1931 by his father, Jean de Brunhoff (1899-1937) who was the maternal
uncle to the future French Resistance fighter, Auschwitz deportee and communist politician
Marie-Claude Vaillant-Couturier (1912-1996) née Vogel.
There was also a slighty older sibling nicknamed Riquet :
Henry Bloch
(1891-1972) who married
Marcelle Marcita Henrieta Frankfurt
(1904-1993) and had four children,
including the literary critic Marie-Claude
de Brunhoff (1929-2007)
who was married for 39 years (1951-1990) to
Laurent de Brunhoff (1925-)
perpetuator of the Babar saga,
created in 1931 by his father, Jean de Brunhoff (1899-1937) who was the maternal
uncle to the future French Resistance fighter, Auschwitz deportee and communist politician
Marie-Claude Vaillant-Couturier (1912-1996) née Vogel.
Following the advice of Professor Sarrus
(who taught them high-school mathematics in 1908-1909) André and Georges prepared together
for the entrance exam to Polytechnique at the
lycée of Besançon, under the excellent tutelage of
Georges Valiron (1884-1955; ENS 1919)
who had this to say about them:

Georges Valiron
|
|
In October 1910, I had both Bloch brothers in my class.
André had already displayed an interest in the abstract properties to which he would
later make such significant contributions.
But he spoke rarely and didn't bother to prepare for the exams.
Georges was more lively and perhaps as good a mathematician as his brother.
Georges was at the head of the class and clearly the best on the written examinations.
André was last in my class of eleven students.
André was lucky and got Ernest Vessiot
to give him the oral exam [for entry into the cole Polytechnique].
Vessiot recognized André's aptitude and gave him a 19 out of 20 on the oral.
|
The two brothers would spend two years (1910-1912) in Valiron's
mathématiques spéciales class of about 11 students.
Both failed the Polytechnique exam on their first try,
in the Summer of 1911.
They were orphaned when their mother passed away on 22 January 1912, 6 months
before the next opportunity.
They probably stayed in Besançon (and in Valiron's class) with
the help of their uncle, as may be implied by the press clipping reproduced below.
Both brothers were admitted to Polytechnique in the Summer of 1912.
André ranked #151, thanks to the exceptional grade from Vessiot. Georges was #229.
André was also brilliantly admitted to
ENS
(13th) but chose to enter Polytechnique with his brother.
They spent a year of military service and had a year of scientific studies.
Then war broke out and they were both called to serve as artillery officers.
After suffering a head injury and losing an eye, Georges was declared unfit
for active duty and returned to Polytechnique in October 1917.
Likewise, André had been assigned to the
117ème régiment d'artillerie lourde
and had fallen from the top of his attacked observation post,
sustaining a head injury which was impairing his return to duty.
So it was that both brothers were in Paris in November 1917...
  On 17 November 1917, between noon and one o'clock,
André showed up for a fateful family lunch at the residence of his aunt and uncle
(an important Swiss watch manufacturer) in Paris,
104 Boulevard de Courcelles. He shot all three guests
(the maid escaped) but his uncle had enough life left in him to put
up a fight and André stabbed him repeatedly with a table knife until
he collapsed (about 50 wounds were reported).
André's three murder victims were:
On 17 November 1917, between noon and one o'clock,
André showed up for a fateful family lunch at the residence of his aunt and uncle
(an important Swiss watch manufacturer) in Paris,
104 Boulevard de Courcelles. He shot all three guests
(the maid escaped) but his uncle had enough life left in him to put
up a fight and André stabbed him repeatedly with a table knife until
he collapsed (about 50 wounds were reported).
André's three murder victims were:
Linda Olivetti was the younger half-sister of the man who founded the Olivetti typewriter company in 1908
(a son of Salvador and his previous wife Elvira Sacerdoti, 1849-1919)
Camillo Olivetti (1868-1943)
whose own son Adriano Olivetti (1901-1960)
would pioneer electronic printing and oversee the development of the
first Italian mainframe solid-state computers, conceived by
Mario Chou (1924-1961): the
Elea series.
About forty Elea 9003 were produced, paving the way for the release in 1964 (!) of the
first commercial desktop computer,
the Programma 101 (P101) of which
44000 units were manufactured over a period of several years; selling in the US for
$3850 each.
Such game-changing technological advances, with a huge future, attracted more than their fair share of nefarious attention and
two wrongful deaths were even suspected by the investigative biographer
Meryle Secrest
(1930-) in her book
The
mysterious affair at Olivetti (2019).
The technological spirit of innovation which the Olivetti family brought to their hometown of
Ivrea (near Turin) arguably survives with
the Arduino® platform, which was invented
in Ivrea too, well after the demise of Olivetti as an independent company.
André didn't resist arrest after the deed. His first words to the police were cryptic to them:
Je me suis vengé de mon état atavique (I avenged my atavism).
André was distressed by the history of mental illness which ran in the family of his mother
(the Didisheim
watchmakers) and blamed it for his own misery. More so than his war injury.
He saw the murders as part of his own eugenic
duty; a way to prevent his uncle from procreating. Or so he said:
It's a matter of mathematical logic.
There had been mental illness in my family.
In his book Des hommes comme nous ( [patients are] people like us)
the psychiatrist Henri Baruk, who served at Charenton,
describes the daily routine which was followed for 31 years by the person he only identified as
the mathematician of Charenton :
"Every day for forty years [sic] this man sat at a table in a little corridor leading to the room he occupied,
never budging from his position, except to take his meals, until evening.
He passed his time [writing] algebraic or mathematical signs on bits of paper,
or else plunged into reading and annotating books on mathematics whose intellectual level
was that of the great specialists in the field. [...]
At six-thirty he would close his notebooks and books, dine, then immediately return to his room,
fall on his bed and sleep through until the next morning.
While other patients constantly requested that they be given their freedom,
he was perfectly happy to study his equations and keep his correspondence up to date."
André Bloch came to the attention of the mathematical community at large through a brilliant
note he sent to Jacques Hadamard (1865-1963)
about paratactic circles, a term apparently coined by
Julian Lowell Coolidge (1873-1954)
in his 602-page authoritative book
A Treatise on the Circle and the Sphere (1916).
Hadamard was so impressed by the note that he immediately proposed a dinner invitation to Bloch,
who said he had to decline but would be delighted if Hadamard could come and visit him instead
at "57 Grande rue, Saint-Maurice".
Hadamard didn't realize until he actually arrived there that it was the address of
the infamous Charenton house
for the criminally insane
(now carrying a lesser stigma as Hôpital Esquirol 12/14 rue du Val d'Osne, 94410 Saint-Maurice).
His situation as a Jewish
inmate in an insane asylum was potentially a dangerous one during the Nazi
occupation of France and Bloch published under the pseudonyms of
René Binaud or Marcel Segond during that period.
Bloch kept up an active correspondance with many well-known mathematicians of the day,
besides Valiron:
Szolem Mandelbrojt
befriended him and was apparently his last visitor before he died from leukemia on 11 October 1948.
Bloch died before the appointment he had with
Binyamin Amira (1896-1968)
who was visiting from Jerusalem.
Among the last works of André Bloch was a 141-page book written with
Gustave Guillaumin (1886-1953; X1905)
a retired ingénieur-en-chef des ponts et chaussées
and former student of Joseph
Valentin Boussinesq (1842-1929).
Guillaumin had been active in research but stopped publishing when he fell ill in 1924.
He was momentarily hospitalized in Charenton too. Their joint work, entitled
La géom trie intégrale du contour gauche,
was published in 1949, by Gauthier-Villars
with a preface by Elie Cartan (1869-1951).
Shortly before his death, André Bloch
was awarded the Prix Becquerel from the French academy of sciences.
(received posthumously on December 13, 1948).
Epilog :
The edifying story of André Bloch is too popular for its own good:
Bloch's theorem
|
Bloch's constant
|
Bloch's principle:
Nihil est in infinito quod non prius fuerit in finito
| | 
Dame Mary Cartwright
|
Dame Mary Lucy Cartwright (1900-1998)
MacTutor
|
Wikipedia
|
Huguenot ancestor
|
Interview
Dame Mary Cartwright (DBE 1969)
obtained her Ph.D. from Oxford
in 1930,
under G.H. Hardy
and Ted Titchmarsh.
She first met J.E. Littlewood as he was sitting in her doctoral jury.
With him, she pioneered the use of
chaos theory in radio engineering (1945).
She was the first female mathematician to be elected (1947)
to the Royal Society.
Mary Cartwright was Mistress of Girton College,
Cambridge from 1948 to 1968 and was knighted in 1969.
She was born on 17 December 1900 at Church Cottage, Aynho, Northamptonshire,
third of the five children of Rev. William Digby Cartwright and his wife, Lucy Harriette Maud,
née Bury. Three days after the
Birth of Quantum Theory.
Two weeks before the Nineteenth Century ended.
Mary Cartwright was descended from the Cartwrights of
Aynhoe Park in Northamptonshire,
next to the village of Aynho
(watch spelling) about 6½ miles southeast of the market
town of Banbury in Oxfordshire,
on the River Cherwell
which meets the Thames at Oxford.
The following paternal lineage of Mary Cartwright is based on her own terse account.
The bracketed numbers before the names of the direct ancestors of [1] Mary Cartwright
are Sosa numbers relative to
her (or her siblings) whereby [2n] is [n]'s father and [2n+1] is [n]'s mother.
Dynasty founder [512] Richard Cartwright (c.1563-1637)
purchased the Aynhoe Park
estate around 1616. His son [256] John was a Roundhead
who stayed in London during the English Civil War.
Aynhoe Park was occupied by
Cavalier soldiers
and John's mother ([513] Mary Egerton, d. 1654) was imprisoned in
Banbury.
After their fateful defeat at the
Battle of Naseby (31 May 1645)
the Cavaliers torched most of Aynhoe Park.
-
[2048] Hugh Cartwright (Nottinghamshire and Northamptonshire)
lived during the reign of Henry VII Tudor (1485-1509). He had three sons.
-
[1024] Rowland Cartwright, ancestor of the Cartwrights of Aynho.
Second of the three sons of Hugh.
-
[512] Richard Cartwright (c.1563-1637)
1st of Anyhoe, married [513] Mary Egerton (d.1654)
daughter of [1026] Sir John Egerton of Egerton.
-
[256] John Cartwright (1614-1676)
married [257] Catherine Noy (d.1644) daughter of
[514] William Noy (1544-1634)
the attorney general to Charles I,
whose advice to levy ship money helped trigger
the English Civil War (1642-1651).
William Noy was the son of [1028] Edward Noye (c.1555-1622) and the grandson of
[2056] William Noye of St Buryan (c.1530-1593)
and [2057] Philippa Noye.
-
John's only son
[128] William Cartwright (1634-1676)
was born in London. He married (1669) [129]
Ursula Fairfax
(1647-1702) daughter of
[258] Lord Ferdinando Fairfax (1584-1648)
and half-sister of
Sir Thomas Fairfax (1612-1671)
who had led the Roundheads to victory at Naseby (1645)
but was also instrumental in the
restoration
of Charles II (1660) which spared him Royalist retribution.
-
[64] Great-great-great-great-grandparents :
Thomas Cartright (1671-1748)
and Armine Crew (d.1728). Married in 1699.
-
[32] Great-great-great-grandparents :
William Cartright (c.1704-1768)
and Byzantia Lane (d. 1738). Married in 1726.
-
[16] Great-great-grandfather :
Thomas Cartwright (1735-1772)
who married [17] Mary Catherine Desaguliers (1747-1814)
granddaughter of the scientist [68]
John Theophile Desaguliers (1683-1744)
who had fled France as an infant (in a barrel, says the legend)
with his father [136] Jean Desaguliers, a
Huguenot pastor who died in 1699.
-
[8] Great-grandfather :
William Ralph Cartwright (1771-1847)
who lived in Rome for a time and then Florence, where he was a correspondent for
The Spectator magazine.
He returned to England and served as a liberal MP for Oxfordshire for
more than forty years. He was married twice and had thirteen children, eight sons by his
first wife and five sons by his second wife, [9] Julia Frances Aubrey,
daughter of [18] Richard Aubrey.
-
[4] Grandfather :
Col. Henry Cartwright (1814-1890)
joined the Grenadier Guards
as an Ensign (1832) rising to the rank of Captain (1846) and
Colonel (1854). He returned to civilian life in 1857 and served as an
MP for South Northamptonshire (1858-1868).
In 1853,
he had married [5] Jane Holbech, daughter of [10] William Holbech (1774-1856) and
[11} Lucy Bowles (c.1781-1835).
Granddaughter of former Banbury MP
[20] William Holbech (1748-1812)
and [21] Anne Woodhouse (d.1830).
-
[2] Father : Rev. William Digby Cartwright (1865-1926) read history at Christ Church, Oxford.
Lived at Church Cottage serving as curate for his uncle the rector
(Frederick William Cartwright) until he became rector himself (1906).
-
[3] Mother : Lucy Harriette Maud Bury (born in 1868, married in 1894).
Daughter of [6] Edward Bury (1821-1880) barrister (name rhymes with "berry") and
his second wife [7] Mary Elizabeth Dowker (1827-1907).
-
[1] Siblings :
John Digby
(1895-1915)
and Nigel, Walter, Henry
(1897-1917).
were killed in action during WWI.
Jane (b.September 1904) married Rev. Hugh Maclean.
William Frederick Cartwright, CBE ("Fred", b. November 1906)
became Deputy Chairman of British Steel.
Cartwright's Theorem (1930)
|
Ph.D. 1930
|
FRS 1947
|
DBE 1969
| | 
A. Adrian Albert
|
Abraham Adrian Albert
(1905-1972)
Ph.D. 1928
|
Math.info
|
MacTutor
|
Wikipedia
|
"A3 and His Algebra"
(A-Cubed)
Chicago's West Side.
A. Adrian Albert obtained his Ph.D. in mathematics from the
University of Chicago in 1928,
under Leonard Eugene Dickson (1874-1954).
He collaborated with the algebraist Lowell J. Paige
(1919-2010).
Dr. Albert was president of the
AMS in 1965-1966.
He authored more than one hundred research papers and seven books:
A. Adrian Albert died in Chicago on
1972-06-06, leaving his wife, née Frieda Davis, two children and five grandchildren.
He had been a member of the University of Chicago faculty for 41 years.
Albert-Brauer-Hasse-Noether theorem (1932)
|
Albert-Paige theorem
|
Papers (1921-2004)
| | 
André Lichnérowicz
|
After gaining agrégation in mathematics (1936) and receiving
his doctorate in 1939, Lichné
became one of the first researchers recruited by
CNRS
upon its creation (1939).
André Léon Lichnérowicz (1915-1998)
Ph.D. 1939
|
Prabook
|
MacTutor
|
Wkikipedia

Lichnerowicz conjecture (1944)
|
cours Peccot (1944-1945)
|
Lichnerowicz formula (1963)
|
Poisson structures (1977)
| | 
Richard D. Schafer
|
Richard Donald Schafer
(1918-2014)
Ph.D. 1942
|
Prabook
|
Gutenberg
He was born on 1918-02-25 in Buffalo, NY, to Edward J. Schafer and his
wife Ruth A. Stone.
Robert was raised in Buffalo and graduated from the
University of Buffalo
(BA, summa cum laude, in 1938 and MA in 1940).
He obtained his Ph.D. in mathematics from the
University of Chicago in 1942,
under A. Adrian Albert (1905-1972).
From 1942 to 1945, Schafer was in the U.S. Naval Reserve, as an Ensign, then a Lieutenant.
In 1945-1946, he was an instructor at the
University of Michigan
in Ann Arbor, Michigan.
Richard Schafer was a member of the
Institute for Advanced Study (Princeton, NJ)
from 1946 to 1948 (and again in 1958-1959).
From 1948 to 1953, he was an assistant professor at the
University of Pennsylvania in Philadelphia, PA.
He was head of the
UConn
Department of Mathematics from 1953 to 1959.
In 1959, Schafer joined the
MIT department of
mathematics as deputy head.
He was appointed Professor of Mathematics in 1968 and became
Professor Emeritus in 1988.
An active member of the
MAA
and the Phi Beta Kappa
honor society, Richard Schafer was elected an
AMS Fellow
in 2013 (at age 95).
Richard D. Schafer passed away on 2014-12-28 in
Lexington, MA (obituary in the
Boston Globe)
five years after his wife of 67 years, the
mathematician
Alice T. Schafer (1915-2009)
née Alice Elizabeth Turner,
who was a longtime professor at
Wellesley College,
a founding member (1971) of the
Association for
Women in Mathematics and a past president (1973-1975).
The two were married on 1942-09-08, shortly after completing
their respective doctorates at the University of Chicago.
Hers was in
differential geometry under
Ernest Preston Lane (b. 1886).
The couple had two sons: John Dickerson Schafer
(Turner, ME)
and Richard Stone Schafer
(Concord, MA).
Nonassociative algebras
|
Alternative
Algebras over an Arbitrary Field (1942)
|
Cayley-Dickson flexibility (1954)
| | 
Jim Terrell
|
Nelson James Terrell, Jr.
(1923-2009)
Terrell Rotation
Born in Houston
on 1923-08-15, to Gladys and Nelson Terrell.
Jim Terrell did his undergraduate work in physics at nearby
Rice University and married
Betty Anne Pearson in 1945.
Three weeks later, the Army sent him to Japan for two years, after which he returned to Rice and
obtained his Ph.D. in Physics in 1950.
He joined the Los Alamos
Scientific Laboratory in 1951.
In 1957, Terrell re-discovered the relativistic optical illusion now known as
the Terrell effect.
(Anton Lampa's 1924 discovery went unnoticed until recently.)
From 1964 to 1966,
he developed the controversial theory that some quasars could have been ejected from
relatively nearby galaxies
(questioning the cosmological origin of their huge redshifts).
In 1970, using x-ray data from the
Vela satellite,
Terrell published a video depicting dying stars, active quasars and the huge temperatures produced by matter
falling into black holes.
Jim Terrell passed away on 21 March 2009.
He was preceeded in death by his oldest daughter, Anne and her husband Paul Argo.
He was survived by his wife Betty, their two younger daughters and two sons-in-law (Barbara and G.J.Hartsfield,
Jeanie and Gregory Lyons)
and their four grandsons: G.J. Hartsfield Jr.,
Kieran Lyons, Avery Lyons and Liam Lyons.

Alexandre Grothendieck
|
Alexander Grothendieck
(1928-2014)
PhD 1953
|
NNDB
|
Wikipédia
Sacha Shapiro (Father)
|
Category Theory
|
Wikipédia

 | |
Yves Glénisson (1962)
|
Yves-Edouard Glénisson (1929-2011)
Doris Glénisson
|
Formules de Glénisson
|
Genealogy
|
Wikipédia
Yves Glénisson was a Belgian mathematician and a trained engineer who
was born in Louvain (Belgium) on May 3, 1929.
He was the uncle of the writer Fabienne "Amélie"
Nothomb
(1966-).
He inherited the title of Roman Count
which had been granted in 1902 to his great-grandfather
Edouard-Antoine Glénisson (1837-1904) by pope
Leo XIII along with the above
arms
(inspired from the Kinschot arms).
Yves Glénisson passed away a few weeks after his eighty-second birthday,
on a Sunday morning, May 29, 2011.

Yves Glénisson never bore his Belgian family arms:
De sable, à la croix pattée d'or cantonnée
de douze abeilles du même, posées en pal.
Yves Glénisson is best remembered for
a new way to compute the roots of a polynomial,
which he published with Léon Derwidué, in 1959.
Yves Glénisson & Léon Derwidué,
Une nouvelle méthode de calcul des zéros des polynômes
Acad. Roy. Belg. Bull. Cl. Sci. (5) 45 (1959) pp. 197-204.
Thanks to Countess
Doris Glénisson (eldest daughter of Yves)
for her private communications and the permission to reproduce the above portrait
of her father.
McNamee
|
Householder & Stewart, 1971
|
Glénisson
& Derwidué, 1960 (pdf, 2485 kB)
Mikhail Leonidovich "Misha" Gromov
(1943-)
Ph.D. 1968
|
IHES
|
NYU
|
MacTutor
|
Wikipedia
|
Genealogy
|
Surname
|
Arms
Born to Leonid Gromov and Lea Rabinovitz Gromov
who gave birth to him in the small town of
Boksitogorsk,
off the WWII front line at the time.
He married Margarita in 1967.
Michael Gromov is a French-Russian mathematician.
What's New?
|
Simons Foundation
Robert Baillie
(c. 1950-)
StackExchange
Robert Baillie
obtained his BS and MS degrees in mathematics from the
University of Illinois at
Urbana-Champaign in 1970 and 1971 and entered a career as a computer programmer after graduation.
He has an experimental approach to number theory,
often using software to unearth conjectures and clues, which sometimes morph into
proofs.
In 1980, Baillie helped develop the
Baillie-PSW primality test,
which is based on the preliminary remark
that no (composite) strong Lucas pseudoprime
is known which is also a
strong Fermat pseudoprime
(although it's conjectured that there are infinitely many exceptions,
none have been found so far).
Summing a Curious Slowly-Converging Series
by Thomas Schmelzer and Robert Baillie
The American Mathematical Monthly,
115, 6, pp. 525-540
(June/July 2008).
Sharing Science on the Web
|
Giants of Science
|
Solvay Conferences
|
Armorial
|
Taupe Laplace
Paul Lévy
|
Nicolas Bourbaki
|
Roger Apéry
|
Lucien Refleu
|
Serge Haroche
|
Other Biographies
External :
Short Biographies
|