How do you want to do it? I suppose you don't want the wreck airborne
(that would be both silly and unpractical).
I'm guessing that you are not considering inflating some device at the surface
of the ocean with long (3800 meters!) cables to pull the wreck.
(Besides, hydrogen is not much better than air for this application.)
So, I assume that your idea is probably along the following lines:
Tie some kind of deflated balloons to the wreck (or put them inside the hull)
and let some kind of liquefied gas evaporate into these until the whole thing lifts up.
Lowering the gas in liquid form (in containers) avoids difficult pumping problems
when it comes to overcoming the tremendous pressure difference
(about 380 times the atmospheric pressure!).
Once the balloon starts going up, its volume will expand greatly because the
surrounding pressure decreases.
In practice (?), you'd have to let some gas out during the ascent so the balloons
won't explode. The maximum amount of gas would be needed at the very bottom,
at a depth of about 3800 meter (12500 ft).
Let's assume the necessary work can be carried out at such depth.
The problem is that the gas is under a pressure equal to about 3800*1025*9.8
(depth x density x gravitation) or about 38.2 MPa (377 atm).
What's the density of hydrogen at such a pressure? Well, hydrogen cannot
be considered an ideal gas (pV=RT) at that pressure, but we may still use the
Van der Waals approximation,
which reduces to:
(p + 3/V2 ) (3V-1) = 8 T
Where p,V,T are expressed using as units the p,V,T values
at the critical point of hydrogen (p=1.293 MPa and T=32.98 K).
The bottom of the ocean is probably at a temperature near the densest point for water (3.98°C)
under normal pressure, so let's us T=277.13 K.
The volume V of a mole of hydrogen at P=38.2 MPa
and T=277.13 K is thus about
x times the critical molar volume of hydrogen, if x is solution of:
(38.2/1.293+3/x2)(3x-1) = 8(277.13/32.98)
Which gives x = 1.024948...
The density of hydrogen near the Titanic wreck would thus be 1/x times
the density at the critical point of hydrogen, which I found listed as 0.031 g/cc.
It's therefore roughly equal to 0.03 g/cc (which is more than 300 times the density
of hydrogen at 1 atm and 0°C).
The density of seawater at the surface is about 1.025 g/cc.
Under 377 atm of pressure, this would increase only by about 2% to about 1.043 g/cc.
All told, 0.03 grams of hydrogen generate 1.013 grams of buoyancy
at the bottom of the ocean and the mass of hydrogen required is 30/1013 or about 3%
of the mass of the whole wreck, if we neglect the self-buoyancy of the wreck.
Taking into account the self-buoyancy of the wreck would probably bring the above number
down to about 2.5%.
I am guessing the mass of the Titanic to be about 10,000 metric tons
(if anybody knows better, please let me know);
2.5% of that is 250 metric tons.
That's a lot of hydrogen!
It would be a lot less if the Titanic was in shallower waters,
but the huge pressure is the killer here!
On 2001-03-08, Bob Cat (USA)
made the following suggestion:
Rather than using a balloon to lift the wreck, run an electrical cable into
the ship and use [electrolysis] to fill it with your choice of hydrogen or oxygen.
|
You do need the same amount of hydrogen whether you put it in a balloon or in the hull
of the Titanic (assuming a broken hull at such a depth could somehow be fixed into something
airtight). You would also need to let gas out during the ascent, or the
hull would almost immediately burst open (just like a balloon would).
The solubility of hydrogen in water is rather low under normal pressure (saturating at
2.14 volumes of hydrogen in 100 volumes of water), but I would
venture a guess that it's much higher at 380 atm of pressure.
If hydrogen is significantly soluble, it can't be used to expel water from the hull,
since whatever hydrogen is produced gets dissolved immediately
(and oozes out of the wreck through whatever opening is left for water itself to be expelled).
Let's not dwell on that particular objection, which may or may not be valid,
and focus only on the main aspect of Bob's comment:
Bob's interesting proposition is to use electricity
to make 250 metric tons of hydrogen from seawater, instead of bringing it to the site in
liquid form. Let's see how much electricity would be needed:
To make a mole of H 2 gas,
it takes 2 faradays of electric charge,
or 192970 C [a coulomb (C) is the charge delivered by a current
of one ampere in a
time of one second ] which is roughly 53.6 A-h (ampere-hour).
What this gives you is just 2 grams of hydrogen.
What you need is about 250 000 000 grams, corresponding to 6.7 GA-h
(6700 000 000 A-h).
To complete the job in a century (876600 hours)
you'd have to run a current of about 7643 A, 24 hour a day 7 days a week.
The delivery voltage at the sea floor should be at least a few volts (I'll
be more precise if/when I find the time to derive the proper dependence on pressure
for the electrolysis of seawater; I've not done this in 20 years and I am rusty on this
particular issue).
Using transformers and AC to DC converters at the sea floor is something you could consider
(it would not be technologically easy) but let's say we stick with
low-tech delivery of straight DC current from the surface...
A length of 3800 m of hefty copper cable ½" in diameter (12.7 mm)
would have a resistance of about 0.5 W.
Even if we use the ocean as a low-resistance return path (so that we only need a single wire)
this means a voltage drop of about 3800 volts!
So, you're gonna use about 30 megawatts (30 MW) of power,
most of it spent warming up seawater...
This is 150% of the power delivered by each of the 4 engines of a 747 jetliner,
24 hours a day for a hundred years!
A Jumbo Jet for 10 Years
If you have the power of the 4 engines of a jumbo jet (80 MW) you'll run a current
63.3% larger (1.633 is the square root of 80/30) and do the job
in "only" 61 years.
You may want to save time and energy by running N identical cables fed with 1/N of your power:
Each cable would be running a current ÖN
smaller than before under a voltage also ÖN times smaller.
The total current in the N cables is thus ÖN bigger
for the same power than it would be with a single cable.
Therefore, the whole job may be completed ÖN times as fast.
With N=100 cables, the job would
thus apparently be completed in "only" 6 years (and 45 days).
Actually, the power lost to the return path becomes
very much relevant at this point (see next comment by Edgar Bonet)
so we would need at least 10 solid years, even with a bigger boat to lessen the
return resistance...
After viewing this page (on 2004-06-14) French physicist
Edgar Bonet
remarked that the resistance of the ocean on the return path could be estimated by
considering the hull of the surface ship through which it
goes to be roughly a half-sphere of radius R = 5 m
(we are gold-plating the thing to avoid corrosion
 ).
This gives a resistance of about 6 mW
(namely, r/2pR, where
r » 0.2 W×m
is the resistivity of seawater).
).
This gives a resistance of about 6 mW
(namely, r/2pR, where
r » 0.2 W×m
is the resistivity of seawater).
This is negligible when we have but a single cable, but roughly doubles
the total resistance when we have 100 of them in parallel.
This also means that there's little to gain by adding many more cables beyond
this point, unless we're willing to use about half of them on the return path...
Lest they become a critical bottleneck,
the bottom electrodes should be quite large too...
Note that each cable has a mass of about 4.3 metric tons, so that the
total mass of copper you need to bring on site to produce the hydrogen
(in ten years) is about twice the mass of the liquid hydrogen you could have brought.
A Jumbo Jet for One Hour
Notice also how
terribly inefficient the whole thing is.
Lifting a wreck of 10000 metric tons
from a depth of 3800 meters requires "only" about 300 gigajoules
(allowing for helpful self-buoyancy).
Using the power of a jumbo jet (80 MW) for about an hour would do
the trick.
(Actually you don't want to do it that fast because you'd have to
fight quite a drag if the wreck is being lifted at 3.8 km/h!)
The hydrogen idea is very wasteful to begin with (because you end up releasing on the
way up almost all the hydrogen you needed to get some buoyancy at the bottom).
If, on top of that, you insist on running
long copper cables (presumably from a nuclear-powered ship) to produce the hydrogen
where it's needed, you end up with a combined efficiency of roughly 0.001%.
Well, that was a nice excuse for some "fantasy engineering"... Thanks, Bob.
"Boomeranging through the Earth" is the title of the fourth chapter
of a 1990 book by 2008)
entitled A Journey into Gravity and Spacetime (Scientific American Library,
ISBN 0-7167-6034-7). In it, Wheeler discusses
the motion of two earthships falling through a shaft
drilled through the center of the Earth. He explains at length that the passengers
of each earthship would experience the weightlessness
associated to a local flatness of their spacetime.
However, they would find out about the curvature
of their surroundings by tracking the relative motion of the neighboring
earthship which shares their fate, 2 seconds ahead (or behind).
On a less philosophical level,
the gravitational "magic" of a shaft drilled through the Earth is also explored in
Chapter 11 of a 1999 book by Robert B. Banks
Slicing Pizzas, Racing Turtles, and Further Adventures in Applied Mathematics
(Princeton University Press ISBN 0-691-05947-0).
Unlike Wheeler (who has the loftier motivations described above)
Banks investigates a shaft which need not go through the center of the Earth.
He quotes the example of a straight tunnel from Washington to Boston,
631.23 km in length, reaching its maximum depth of 7.82 km at
its midway point, directly under New York city.
Banks needlessly skips some of the elementary theoretical part, which we outline below.
The basic idea is a part of scientific folklore whose exact origins remain unknown.
Let's ignore completely the rotation of the Earth and assume it's simply
a perfect homogeneous sphere of radius R whose surface gravity is g
(in the absence of any rotation, g would be close to 9.82 m/s2; slightly higher than
the standard value).
Before you start raising funds for the actual project, consider just one of the
many issues which make it absolutely impractical:
The center of the Earth is actually hotter
than the surface of the Sun.
By Gauss Theorem applied to gravity
(instead of the mathematically similar electrostatic field) we see that
the centripetal gravitational field inside the Earth is proportional
to the distance r from the center.
It is equal to g r / R.
Assume a straight tunnel exists (shown in red in the picture below)
between two points on the surface
of the Planet and that we can drop an object (a marble or a passenger vehicle)
which can slide without any friction along this tunnel.
This object starts with zero speed and can be later retrieved as it
emerges on the other side of the tunnel, also with zero speed.
Gravity accelerates the thing until the tunnel's maximum depth is
reached (at a point H located at a distance a from the
center O of the Earth) and decelerates it beyond that point.
This looks like a nice fantasy ride... Let's see how long it would take:
Let M be the position of the vehicle.
If q is the angle from OH to OM,
the vehicle's distance to the center of the Earth
is r = a / cos(q).
The component of the gravitational acceleration along the direction
of the the tunnel is:
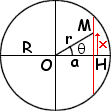
- g r sin(q) / R
=
- g a tan(q) / R
The above is the second derivative of
x = HM = a tan(q).
Therefore,
x'' + (g/R) x = 0
Surprisingly enough, the motion inside the tunnel is thus found to be an
harmonic
oscillation which does not depend on the parameter a (which
characterizes the position of the tunnel).
The motion's "period" (twice the travel time from one end of the tunnel
to the other) does not depend on the "amplitude"
(which is half the length of the tunnel).
In other words, this type of transportation allows "free" travel between two
points on the surface of the Earth in a constant time equal to:
p Ö(R/g) =
2530.4187 s
That's about 42 minutes and 10 seconds from
here to any point on the Globe.

