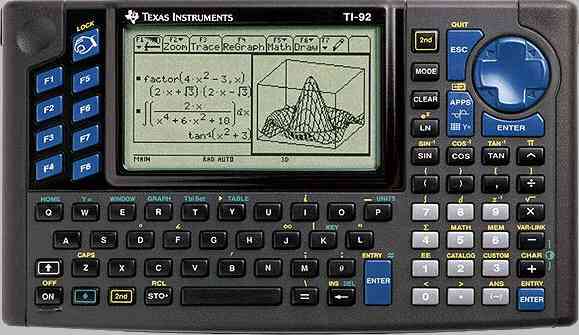
|
home |
index |
units |
counting |
geometry |
algebra |
trigonometry |
calculus |
functions
analysis | sets & logic | number theory | recreational | misc | nomenclature & history | physics |
Final Answers
|
Related articles on this site:
- Algebra.
- Nonprogrammable calculator from Texas Instruments: TI-36X Pro.
- Hewlett-Packard programmable calculators: HP-49g, HP-49g+, HP-50g.
- HP Prime: Hewlett-Packard's leading graphing calculator, since 2013.
- The HP-35s: Programmable RPN calculator authorized in NCEES exams.
- Sharp EL-W516: Nonprogrammable scientific calculator for education.
- Casio calculators for science class: fx-115es = fx-991es = fx570es.
- Canon F-792SGA: Four-line nonprogrammable scientific calculator.
- Bézout's Theorem: bezout(x,y) function for a TI-92, TI-89 or Voyage 200.
- Calendrical functions: Gregorian and Julian calendars on a Voyage 200.
- Calendrical functions: The Hijri calendar on a TI-92, TI-89 or Voyage 200.
- Units of measurement: Time, length, area, volume, mass, etc.
- The proleptic SI system: The atomic second and 6 dimensionful constants.
- Primary conversion factors between customary systems of units.
Related Links (Outside this Site)Wikipedia: Calculators, TI-92 series, TI-89 series.ticalc.org : TI-92, TIGCC news Techno-Plaza: TI-68k Programming TI-92, TI-89, TIGCC Assembly Lessons. The Ultimate TI Calculator FAQ by Patrick Davidson. Newsgroups: bit.listserv.calc-ti (TI calculator users). Bhuvanesh's TI-89 / TI-92 Plus / Voyage 200 page by Bhuvanesh Bhatt. Alvasoft: Truc & astuces pour TI-89, TI-92 et Voyage 200 (in French). Maths en Prépa by Jean-Michel Ferrard (Lycée St. Louis). TI Calculators at calculators.torensma.net by Elmer Torensma. Nutshell (leather cases for handheld calculators). The Museum of HP Calculators | HP 35 Algorithms by Jacques Laporte DMOZ: TI Graphing Calculators |
The same scheme is used to obtain accented letters as a secondary function of the vowels (except i) most often associated with the relevant accent (in French). For example, a [2nd][E] prefix will give you an accute accent. There are a couple of orphan double-modifiers for the French cedilla (çÇ) and the Spanish tilde (ñÑ) using the "C" and "N" keys, respectively. Type [2nd][C][C] for "ç".
Undocumented Keyboard Combinations :There are so many possibilities with modifier keys that some implemented ones may not find their way into the technical documentation. For example, on a Voyage 200 [diamond][LN] gives the decimal log function (which accepts an optional second argument to specify a base other than 10). Similarly, [diamond][^] gives the two-argument root function, which raises its first argument to the power of the reciprocal of the second one [e.g., root(x,3) is the cube root of x]. Those two features are also respectively obtained via the [diamond][7] and [diamond][9] keyboard combinations, which are properly documented (but far more difficult to memorize, if you ask me).  (2007-05-17)
Built-in and User-defined Physical Units (2007-05-17)
Built-in and User-defined Physical Units
A great afterthought, with a few rough edges. The original TI-92 did not include built-in physical units. This nice add-on came only with the introduction of the "plus" module and became part of the TI-92+, the TI-89 and the Voyage 200 handheld calculators. As implemented now, the feature still suffers from a few poor design choices, hastily made when physical units were introduced as a mere afterthought. Essentially, units are system variables defined in terms of a few of them which are permanently undefined and considered "basic" (by default, these basic units are the fundamental SI units, but the calculator allows you to change that). New units can be defined by assigning a value, in terms of previously established units, to a "system variable" (such variables have names starting with an underscore and are always accessible, regardless of current working folder). For example, the typographical point can be precisely defined from its legal equivalent in inches: 0.013837 _in ® _point
To view the value of 12 points in millimeters (namely, 4.2175176 mm)
you simply use the
conversion operator (the right-pointing triangle
"
The predefined customary units of length are (correctly) based on the 1959 international inch, forever tied to the metric system (25.4 mm to the inch). The US Coast and Geodetic Survey uses the former US equivalence of exactly 39.37 inches to the meter. So, in the unlikely event that you need the utmost in precision from "survey data", you may want to define special "survey units" like:
1 _m / 39.37 ® _ins
25.4 times 39.37 is exactly 999.998. So, the ratio _in / _ins is exactly 0.999998. An inch is just 2 ppm less than a "US Survey" inch. If you don't like that "s" suffix, use your own naming scheme. Greek letters are normally allowed in unit names (and/or other TI-92 identifiers). However, TI's backup/restoration software may sometimes choke on them (I could not restore a "G5" variable without changing its name first). You may even introduce new dimensions by referring to units that are not otherwise defined. For example, the SI unit for radiological doses is the sievert (symbol "Sv") which is not expressible in terms of other SI units. It's commensurable with the rem unit (Röntgen equivalent for Man). Although neither unit is predefined or definable, you may still specify their relationship as follows (unfortunately, we can't capitalize "_Sv").
0.01 _sv ® _rem
Thereafter, the conversion operator
" That basic design is nice and correct: Units translate into dimensions attached to numbers. This specifies the physical meaning of a numerical quantity. Such dimensioned quantities can be displayed painlessly using any commensurable unit, without the risk of errors. New custom units defined as system variables are smoothly integrated into the set of predefined units. So far so good... Volatile user-defined unitsFor some obscure reason, user-defined units can't be locked or archived like other variables. This allows inadvertent modifications of their values which may mess up "silently" many unit computations for a long time. The risk is heightened by the fact that the assignment operator and the unit conversion command are both right-pointing arrows which could be mentally mistaken for each other. TIP: It's a good idea to put all your unit definitions in a program of your own (I called mine "reset") along with the definition of your custom menu and anything else which you might want to restore in case the content of you calculator's RAM is lost for any reason. You can "archive" such a program into flash memory and run it to recover from a power failure. I execute this "reset" of mine just before any critical computation with custom units, just in case... Conversely, there's no easy way to correct the minor mistakes (presented below) which occur with several built-in physical units. CapitalizationUnits are system variables with a special typography (their names start with an underscore character). As such, they inherit the TI-92 input convention which treats UPPERcase letters in identifiers just like their lowercase counterparts. Unfortunately, this won't accomodate user-defined units with critical capitalization of SI prefixes, like m- (milli-) vs. M- (mega-). Predefined units are mercifully displayed with the proper capitalization (e.g., "_MHz" is shown when "_mhz" has been typed) but user-defined units are shown only in lowercase. Case-dependent keyboard input is notoriously error-prone. It's thus probably a very good thing that TI equates all identifiers that are uppercase or lowercase variations of each other. However, it would have been nice if the output name of all of these mirrored the capitalization chosen by the user when the corresponding variable was last defined, redefined or cleared. Too bad it ain't so. Name LengthTI's documentation states that the name of a variable is 8 characters or less, which limits the length of unit names to 7 characters after the leading underscore. This would allow the Persian mesghal (a mass unit worth 4.6083 g) to be defined via: 0.0046083 _kg ® _mesghal At first, this works nicely. However, such a 7-character unit name will appear thereafter incorrectly as "_mesghalR*" on the menu of mass units, in which it becomes an invalid choice. This seems to be only a bug in the management of the catalog of units, but it's enough to further restrict the names of user-defined units to 6 meaningful characters or less. Too bad for the mesghal, whose usual symbol ("Ms") can't be used either, because of the aforementioned capitalization issue ( _Ms would conflict with the built-in millisecond unit _ms for "ms"). Some poor choices of predefined unitsThe aforementioned problem with capitalization means that the commendable use of _c for Einstein's constant (the natural unit of speed) precludes the use of the capitalized symbol _C for the coulomb (the SI unit of electrical charge). For the coulomb, a nonstandard built-in substitute (_coul) was thus introduced which is not properly capitalized. (Although the name of a unit is never capitalized in English, the symbol for any unit named after a person is always capitalized.) Some physical constants share the same status as ordinary units. Unfortunately, this includes Coulomb's constant under the symbol _Cc which prevents the more useful use of _cc for "cubic centimeter" (a very common unit of volume). Much worse: _G is used for the standard acceleration of gravity (which is called a "grav" as a unit of acceleration, by the way). This prevents the highly desirable use of _g for gram (the very dubious symbol _gm being used instead). The symbol _k is used for Boltzmann's constant, which rules out _K for the kelvin (the SI unit of thermodynamical temperature). This perpetuates the use of _°K for the kelvin unit, which encourages the deprecated locution "degree Kelvin" instead of the correct (lowercase) name "kelvin" for this proper SI unit. Oh, well... Slight mistakes in the precise values of some unitsSome rigorous discipline is required to identify the proper value of a unit in delicate cases. The TI designers did not exercise enough care in that regard. One example is the value of a "year" as a unit of time. The only acceptable "year" unit is worth exactly 31557600 seconds (365.25 days of 86400 atomic seconds each) and is equal to 1/100 of the Julian century, which is itself routinely used by positional astronomers to describe secular motions. This scientific year unit is only very roughly equal to a tropical year (which is a decaying interval not suitable as a proper unit of time). The TI designers used instead a rounded value of the tropical year at epoch 1900.0 (sometimes misleadingly dubbed "ephemeris year") namely: 31556925.9747 s. Although that value appears in a former astronomical definition of the second, it was never meant to be a unit itself and was never used in that capacity by anybody (although it does appear in the catalog of units of the HP-28 calculator). This erroneous value for the "year" (_yr) entails an erroneous value for the built-in "light-year" (_ltyr) as well... The Torr and the mmHg are two units of pressure which are interchangeable in practice. However, there's technically a 0.14 ppm difference between them. The mmHg (pronounced "millimeter of mercury") is based on a conventional density of mercury defined to be 13595.1 g/L. On the other hand, the Torr (named in honor of Evangelista Torricelli) is defined to be 1/760 of a standard atmosphere of 101325 Pa (which, incidentally, was itself introduced by the 10th CGPM in 1954, as the rounded down value of 760 mmHg).
The TI designers chose to equate both units with 133.32236842105 Pa and they failed to properly capitalize the Torr symbol (using "_torr" instead). Needless downgrading of all conversions
When conversion factors between units are known to be exact fractions
(including statutory decimal fractions)
conversions should not entail any loss of precision or any
"automatic" downgrading (from an integer or a fraction to a
floating-point value).
Yet, since conversion factors are only stored
as floating-point values, exact values
are systematically downgraded in any conversion.
Downgrading should not occur unless unavoidable or explicitely
requested by the user for a specific computation
Dimensions missing from catalogUsers can't define new categories (physical dimensions) in the unit catalog. So, some units are unlisted orphans. Examples of excluded dimensions include: Mass density (mass per volume, like pcf = lb per cubic foot). Linear density (mass per length, like tex = g/km and denier = tex/9). Flow rate (volume per unit of time)... Also, the catalog of units seems to be managed extremely inefficiently. (Inefficient sorting in quadratic time, or worse?) After defining only about 3 dozens custom units, I have to endure a very sluggish response time: It takes several seconds for the catalog to show up. This highly practical but undertested feature was clearly not a priority for the TI designers (see the above related bug concerning names for units with 7+1 characters). At the very least, there should be a predefined catch-all "miscellaneous" category for all orphan units, built-in or user-defined. Otherwise, it might not be so easy to find out that "_A" is the built-in symbol for ampère (electrical current) which makes "_a" unavailable as a user-defined symbol [for example, to introduce the scientific year (whose international symbol is "a" for annum) as a replacement for the dubious built-in "_yr" unit discussed above]. Entropy (energy over temperature) could be featured prominently as the physical dimension commensurate with both heat capacities and units of information. That would be a great educational epiphany for most calculator users, who would thus discover the physical nature of information. Until such time as this becomes a built-in feature, here's a minimal way to plug the better part of the hole (_meg is slang for "MB" or "megabyte"). This uses the built-in value of Boltzmann's constant (_k) and skirts the unpalatable legal efforts to decimalize the binary multiples of the bit used and loved by engineers and others:
_k ln(2) ® _bit
Conclusion
The introduction of physical units was a nice
improvement to the original TI-92, but many of the above issues should have
been better addressed and/or corrected with the sofware updates which followed
the introduction of this great feature.
Although the basic design is sound, it would have been a delight to find more
polished details about physical units in this wonderful TI calculator.
Discontinuity cliffs appear in the complex extensions of some functions. This is not a problem with the TI calculators. Rather, it's a fact of mathematical life that there's no continuous way to extend to the complex realm some quantities defined for positive real numbers, including square-roots and logarithms. By default (factory setting) titanium calculators don't extend the domain or the range of real analytical functions to the complex realm. This is what the factory setting "1: REAL" really means in the "Complex Format" item on the first page of the MODE menu. You get an error message if you attempt to obtain the sine of an imaginary number or the square root of a negative number... Unfortunately, you can't enjoy the former (which should be unrestricted) without also allowing the latter (which may present huge problems). 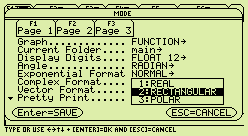 To allow the built-in analytical functions to become complex functions of a complex variable, you must pick one of the other two choices. For example, choose "2: RECTANGULAR" if you want complex results to be displayed in the usual Cartesian format, as x+yi. 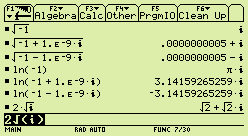 For entire functions (like exp, sin or cos) this works smoothly. However, multivalued functions, like Ö or ln, must feature an unavoidable cliff of discontinuity. As implemented on titanium calculators, both of those functions exhibit a jump discontinuity as one crosses the demi-axis of negative real numbers (see above screenshot). 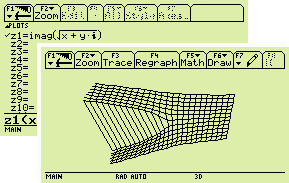 The screenshot at right presents the cliff in the imaginary part of that particular implementation of the square root function (the real part is continuous). The face of the cliff at negative real values of x+iy is a parabola of equation:
z 2 = -x
0 to the 0th power should be 1. ¥ and +¥ shouldn't be equal. Zero to the power of zero is equal to unity for at least two important reasons (among many others). The first of these is that an empty product must be equal to unity (1) for exactly the same reason that makes an empty sum equal to zero: The value of the sum of no terms cannot depend on the value of any term, yet the value of a sum of n+1 terms is always obtained by adding one term to the sum of n terms, whether n is zero or not. Another compelling justification is that polynomial functions of a real variable (linear combinations of nonnegative integral powers of the variable) must be continuous functions! There's no discontinuity at zero and absolutely no reason to introduce one. (By contrast, the function of two variables "x to the power of y" has an essential discontinuity at (x,y)=(0,0) although it does have a well-defined value there, namely 1.) Generations of secondary-shool teachers have been teaching that 00 ought to be undefined. This mistake has found its way into almost all textbook at the secondary level. People in higher education know that it ain't so, but they rarely bother to point it out. Unfortunately. 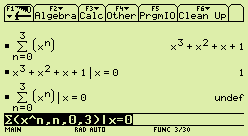
This misconception sneaked into the design of the electronic calculators we're discussing here:
Shown at right is one inconsistency caused
by the fact that the Voyage 200 chooses to
ignore that 0 to the 0-th is well-defined (and equal to 1).
Infinities:The Texas Instrument calculators deal mostly with real numbers. The pseudo-numerical infinities implemented are thus essentially only the two signed infinities -¥ and +¥ although the latter is just denoted ¥ (a symbol which competing Hewlett-Packard calculators properly reserve to the algebraic unsigned infinity defined in the complex realm as the directionless representation of the entire infinite circle at the horizon of the complex plane. Consequently, 1/0 (which is normally equal to unsigned infinity ) is rightly considered undefined (the symbol undef is used). Unfortunately, the way the symbol undef itself is handled algebraically by the calculator is dubious at best, with little or no evidence for consistent design. It does seem that an algebraic expression involving undef always evaluates to some expression containing undef but the result isn't necessarily undef itself (as it should). Titanium calculators are powered by Motorola's 68000 microprocessor. The descendants of the TI-92 (but not the original TI-92 itself) include a function called Exec which executes directly a string of hexadecimal digits as machine language code. It's very risky to do so even if you think you know what you're doing. Back up your calculator and be prepared to restore it if you experiment with this... I am providing safe examples, but they must be typed right ! The Simplest Assembly ProgramHere's the shortest possible well-formed 68000 program: 4E75 OK RTS It contains just a single instruction (RTS) which tells the 68000 processor to "return from subroutine". The microprocessor would do that by pulling from its system stack whatever return adress was pushed there as the routine was called, using a "jump to subroutine" instruction like JSR OK or BSR OK. This lets the processor proceed with whatever instruction follows that particular JSR or BSR. In this, "OK" is merely an arbitrary label which stands for whatever address (location in the computer's memory) our sample program is stored at. This allows other assembly instructions to refer to that particular address. Part of the job description of the piece of software called an assembler is to figure out what values are assigned to such labels. Those values are then used to generate the actual numerical code corresponding to the assembly instructions, which are allowed to use labels as parameters. The assembler translates assembly instructions into machine language directly executable by the processor. For the 68000 family of microprocessors, this takes the form of a sequence of 16-bit operation codes (opcodes) possibly followed by one or two 16-bit words of additional data pertaining to that particular operation (if present, this is sometimes known as immediate data, whereas data nested within the opcode itself can be dubbed quick data). In our simple example, it's just a matter of looking up the Motorola documentation for the opcode corresponding to the lone RTS instruction, namely 0100111001110101 in binary or 4E75 in hexadecimal. We put this in the first column of the above, to mimick what the output listing produced by an actual assembler would be. To execute this code on one of the TI-92 descendants, just type in: Exec("4e750000") This does absolutely nothing, of course, but it's a safe demo of the use of Exec. A trailing "0000" word in executable strings is necessary to avoid an error message which reads: "Invalid relocation data in ASM program". Let's get a taste of actual assembly programming by writing a slightly less trivial self-contained 68000 program, which we shall also assemble "by hand": Assembling bit by bit, without an assembler...The following routine, labeled "TIMER", executes a simple loop ten million times. By measuring its running time, you may determine the clock rate of your calculator. 203C TIMER MOVE.L #$989680,D0 0098 9680 5380 LOOP SUBQ.L #1,D0 66FC BNE LOOP 4E75 RTS As before, the leftmost column (normally provided for you by the assembler itself) shows in hexadecimal the numerical codes which result from assembling the instructions shown to the right. Let's do the job of the assembler... The "TIMER" label is the normal entry point of our short program, provided for external references to it. The "LOOP" label, on the other hand, is a reference used internally, at the third line of this piece of assembly code. Following the TIMER label on the first line is an instruction with an "L" attribute. Such an attribute indicates what data size is involved, among only 3 possibilities: B for an 8-bit byte, W for a 16-bit word, L for a 32-bit long word. The instruction itself is called MOVE and says that a piece of data of that size has to be moved from one location (source) to another (destination). Those locations are specified by the two "operands" which appear on the rest of the line. The source is given first and the destination must be a location whose contents can be modified... Here, the source is #$989680. The prefix "#" says that we're dealing with so-called "immediate" data located just after the code for the instruction being executed. The dollar sign "$" indicates that the value is given in hexadecimal. $989680 is the hexadecimal representation of the decimal value 10 000 000 (as advertised, we want to execute a small loop ten million times). So, we put that 32-bit data right after the opcode for MOVE (itself put together as explained below). We start with the most significant 16-bit word ($0098) followed by the least significant word ($9680). For processors of the 68k family, lower addresses in memory do correspond to higher-order bytes (some processors use the opposite organization, including the 6502 which powers Apple II computers). How do we obtain the code for MOVE itself? Well, the Motorola documentation gives the details: The 16-bit pattern for a MOVE operation starts with the two bits 00. The next two bits indicate the data size: 10 is for L ("long"). The next 6 bits indicate the destination of the data, which is encoded as 000000 for the D0 register specified here. To specify that the source is "immediate data" (in the sense discussed above) the last 6 bits should be 111100. All told, the bit pattern must be 0010000000111100 or 203C in hexadecimal, as shown leftmost. The next operation SUBQ is encoded in a single word (Q is for "quick") because the small "immediate" data it involves occupies 3 bits within the operation code itself. The 16-bit pattern of SUBQ starts with 0101 followed by the 3-bit data 001 for #1 (note that 000 encodes #8, since there's clearly no need to use this operation to subtract zero). Then a single "1" bit followed by 2 bits for the data size (here 10 for "L") and the 6 bits indicating the destination (here 000000 for the D0 register). All told, the binary pattern is 0101001110000000 or $5380. The BNE insruction means "branch if not equal [to zero]". It tells the processor to check its "Z" bit (which is set by the previous SUBQ operation if and only if the result stored in the D0 register is zero) and go to the specified excutable address (i.e., LOOP) if Z is not set. Otherwise, the processor proceeds with the next instruction (RTS). This has the desired effect of looping ten million times by decrementing the content of the D0 register until it's zero. The code for BNE consists of a $66 byte followed by a byte whose value is the difference between the location following the opcode (here, that's where the RTS instruction lives) and the location to jump to in case of a successful test. In this case, we'd need go back 4 bytes (to the SUBQ instruction) so the displacement is $FC (i.e., the byte-wide two's complement representation of -4). The whole opcode is thus $66FC. All legal displacements encoded within the opcode are nonzero even bytes. A zero byte or an $FF byte would specify, respectively, 16-bit or 32-bit displacements given as "immediate" data following the opcode. As always, the "subroutine" ends with an RTS instruction (opcode $4E75). For other examples short enough to assemble by hand, see my own highly optimized way to convert calendar months into days, and vice-versa. The core of each process takes only 5 words of 68k code! I also show how to extract a square root in just 16 words of code... Run the above by typing in the following command. No typos allowed! Exec("203c00989680538066fc4e750000") On my own Voyage-200, this takes about 14.5 s, including a launching overhead which can be estimated by experimenting with different numbers of iterations (e.g., $05F5E100 = 100 000 000) using a method presented in the next article. This boils down to 1.423 ms per iteration. From this, we may work out the frequency of the system clock which paces the microprocessor (it's quoted between 10 MHz and 16 MHz for this class of calculators). The MC68000 timing data tells how many clock cycles each instruction takes to execute, namely: 8 cycles for SUBQ and 10 cycles for BNE (when the branch is taken). That's a total of 18 clock cycles per loop. The duration of each clock cycle is thus 1423 / 18 = 79 ns. The reciprocal of that time is the clock frequency: 12.65 MHz. To make computations trivial and to improve timing accuracy, we may design a routine which takes exactly 1000 000 002 clock cycles, so that it executes in as many seconds as there are nanoseconds (ns) in the basic clock cycle! (Be prepared to wait a minute or two.)
time code
---- ----
12 203C TIMER MOVE.L #55555554,D0
034F
B5E2
8*N 5380 LOOP SUBQ.L #1,D0
10*N 66FC BNE LOOP
2
16 4E75 RTS
To make the whole thing about 10 times as fast and allow the precise "overhead cancellation" described in the next article, we would use N = #5555554 = #$0054C562. This indeed represents a difference of 50000000 (in decimal) with the previous value of N (count the 5's) which appears directly in the above assembly instructions and indirectly in the timing column. That difference translates into a running time of exactly 900 000 000 fewer clock cycles, regardless of whatever fixed overhead may exist when either version of the routine is called. (That's the origin of the exactness of the "divide by 0.9" instruction which appears in the improved version of the following recipe...) A simple recipe based on the previous assembly example. On a TI-92+, TI-89 or Voyage 200 handheld calculator, clear your home screen and type in the following command. Typos could mess up your calculator!
Exec("203c034fb5e2538066fc4e750000")
Be prepared to time that with a stopwatch, which you start as you press "ENTER" and stop when the input line becomes highlighted again (as it does after any computation). You may take a nap for the first minute or so... The time in seconds is nearly the duration of your clock cycle in nanoseconds (ns). The clock frequency (improperly known as "speed") is the reciprocal of that number. For example, a time of 1 min 20 s (i.e., 80 seconds) corresponds to a clock cycle of 80 ns and, therefore, a clock frequency of 12.5 MHz. More accurate results, with error compensation :It takes more than a third of a second for your calculator to parse your input line, launch the assembly program and return after its execution. Also, there's your own reaction time in operating the stopwatch. The following method eliminates the first source of timing error completely and may reduce the second one drastically. Proceed as above with the following command, which is about 10 times faster.
Exec("203c0054c562538066fc4e750000")
Subtract the time obtained (in seconds) from the time obtained in your first measurement and divide that difference by 0.9. The result in seconds is equal to your clock cycle expressed in nanoseconds (ns). If you divide that result into 1000, you obtain the clock frequency in megahertz (MHz). This method corrects the previous rough estimate to 0.1% accuracy or better. With my own Voyage 200 PLT handheld calculator, I obtained the following results for the first measurement, repeated 4 times to check my own consistency: 79.39 s 79.24 s 79.35 s 79.35 s For the second measurement: 8.24 s 8.27 s 8.29 s 8.25 s Throwing out high and low and retaining the average of the rest, I obtain 79.35 and 8.26. The difference is 71.09. Divided by 0.9, this gives a clock cycle of 78.99 ns and, therefore, a measured clock frequency of 12.66 MHz. That's very close to the 12.65 MHz. result I obtained a few days ago on that same calculator, with a different set of measurements (0.1% estimated accuracy). Come to think of it: This might make a nice classroom activity. A good question to ask the students is this: From their results (or the above results) what's an estimate of the fixed "overhead" time whose influence is eliminated by the above error-compensation method? How many clock cycles does that represent? Answer (with the above data): 0.36 s. 4.6 million cycles. That's the time it takes to execute over 200 000 instructions. What could the processor be busy doing? I don't have the answer to that question !
Why don't you
send
me your own measurement results [second method only]
with details about your handheld (upgraded TI-92, TI-92+,
TI-89, Voyage 200 ) including the approximate date of
purchase and/or manufacture, so I can post the details here and
tell the World about the actual speed of TI calculators...
On newer machines, hardware and software info is at item A (About..) of the F1 menu from the home screen. On any machine, the copyright notices and the dated version number of the software are obtained by bringing up the I/O screen (press F5 from the home screen) and pushing the diamond modifier followed by an opening parenthesis (push [diamond][home] to return to the home screen). Here's what I get on my original TI-92 from 1995: Copyright @ 1995 Texas Instruments, Inc Copyright @ 1995 Soft Warehouse, Inc. Copyright @ 1995 UJF-CNRS Version 1.3 October 20, 1995 Early ROM versions include: 1.0b1 (13 Sept 1995), 1.2 (11 Oct 1995), 1.3 (20 Oct 1995), 1.4 (17 Nov 1995), 1.5 (2 Jan 1996), 1.7 (18 Jan 1996), 1.8 (28 Feb 1996), 1.10 (20 March 1996), 1.10 (26 March 1996), 1.11 (11 Apr 1996), 1.12 (8 May 1996), 2.1 (19 Aug 1996). The latest (downloadable) revision for my Voyage 200 reads: Copyright @ 1998 Texas Instruments, Inc Copyright @ 1998 Soft Warehouse, Inc. Version 3.10 07/18/2005 The language supplied with TI-92, TI-89 and Voyage 200 calculators. For lack of a better name, Texas Instrument and TI users call BASIC the built-in programming language which comes with the TI-92 and its descendants. However, this bears little resemblance with the amorphous BASIC language (an acronym for Beginner's All-purpose Symbolic Instruction Code ) which was so popular at the beginning of the microcomputer era and which featured mandatory numbers on every line (thus encouraging the infamous GOTO instruction). What TI offers is a nice little language which can exploit the handheld calculator's resources with a sufficient set of control structures. User-defined functions can be recursive (i.e., a function may call itself). That's rare on a handheld. How efficient is BASIC? Well, let's use a compensated timing of an empty loop, like we did above with 68k machine language. Just time the following commands: For i,1,1000:EndFor For i,1,10000:EndFor On my aforementioned 12.66 MHz handheld, those take respectively 6.17 s and 58.34 s. The difference is 52.17 s. The time per iteration is 1/9000 of that, or nearly 5.797 ms. This corresponds to about 73400 clock cycles or roughly 3000 microprocessor operations. This is indicative of the inefficiency of the interpreted BASIC instructions compared to similar machine language functionality. Estimating clock frequency without an assembly program :The timing of the above benchmark on my brand new 12.66 MHz Voyage 200 handheld calculator can be used to devise a command whose running time in seconds gives the duration of the system clock cycle in nanoseconds, namely: For i,1,13571:EndFor On my old (1995) original TI-92 handheld calculator, this takes 133.4 s, which indicates a clock cycle of 133 ns and a frequency of 7.5 MHz (not 10 MHz). Unlike our recommended method, which depends only on the machine's hardware, this approach depends critically on the software which interprets BASIC commands, which might vary (although TI probably won't touch it). However, they must be entered or edited as a single line. This is a strange situation for the line of calculators that pioneered the nice two-dimensional display of equations in the fisrt TI-92 model (pictured below) back in 1995. In practice, mono-dimensional editing of algebraic expressions isn't much of a hindrance, but it seems to bother a whole generation of new users who have been spoiled by direct editing of those pretty two-dimensional displays. (That feature is available not only on the top calculators of TI's competitors but also on inexpensive educational calculators.) Also, many professionals simply prefer linear editing of algebraid expressions and will revert to it if given a choice (which they often are). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||