In his unpublished manuscript Algorismus Proportionum
(probably written between 1356 and 1361)
Nicole d'Oresme (1323-1382) made several
important mathematical innovations, including
fractional exponents.
Considering only positive quantities, Oresme realized that the cube root of x
could usefully be considered as x raised to the power of 1/3.
The square of that would then be x raised to the power of 2/3.
He thus defined raising to the power of p/q as the q-th root of
a p-th power (or vice-versa).
Oresme went as far as to suggest that the exponent
could even be an irrational number, because the
resulting power could be obtained with arbitrary precision using rational
approximation of such an exponent.
At the time, Oresme's innovation was revolutionary.
Powers (mostly squares and cubes) had previously been used to obtain
the proper measurements of surfaces or solids (area and volume, respectively)
from linear measurements of their sizes (length).
What Oresme offered was an analytic perspective on the concept of exponentiation
which had no geometrical counterpart...
... or so it seemed for a few centuries. Read on.
Informally, the notion of a measure is based on the following features:
- The measure of an object is a
nonnegative number assigned to it.
- The measure of two disjoint objects is the sum of their measures.
- Two congruent objects have the same measure.
If the first requirement is dropped (as is the case for the
chi characteristic, which is otherwise similar to
a measure) then no well-defined notion of dimensionality can be based
on the resulting semi-measure.
Refinements of the second of the above statements (to accomodate infinitely many
objects, not necessarily disjoint) is the crucial concern of classical
measure theory.
The third statement depends entirely on what is meant by congruent.
At the very least, in linear geometry, two objects that
are obtained from each other by translation are congruent.
It's not at all trivial that objects obtained from each other by rotation
are then necessarily congruent.
Arguably, a fourth statement more directly connected to dimensionality should be
considered: The measure of a cartesian product is the product
of the measures of the components. This seems especially important for a
consistent generalization of the chi semi-measure.
Loosely speaking, in a vector space, if scaling an object
by a factor k turns it into an object whose nonzero measure
is kd times as large, then that object has
dimension d. For example, scaling an ordinary surface makes the measure
of its area
k2 times as large and its dimension is thus d = 2.
Scaling a Koch curve by a factor 3 turns it into
an object whose measure must be 4 times as large (because it's composed
of 4 congruent copies of the original object). So, the dimension d
of the Koch curve, if it is defined at all, must be such that:
3 d = 4
Therefore:
d = log 4 / log 3 = 1.2618595...
Von Koch's snowflake is the closed curve
obtained by assembling 3 of the above in a triangle:
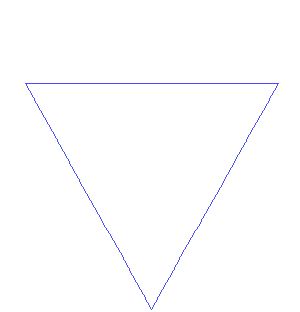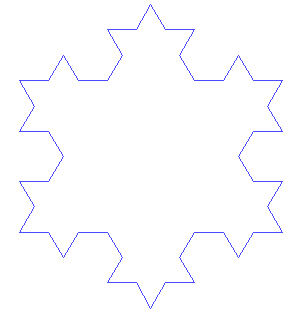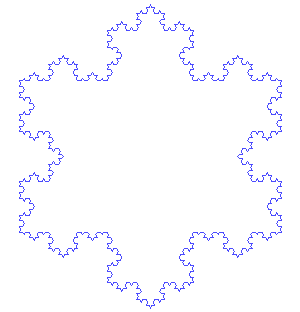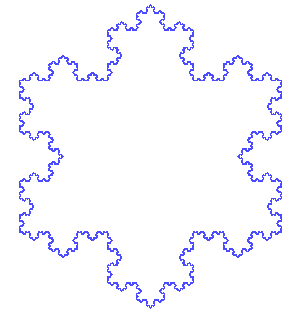
Incidentally, the surface area enclosed by that curve is fairly
easy to compute. Observe that the number of sides of the
shape is multiplied by 4 each time; it's equal to 3 4n
after n steps.
At each step, the added surface area consist of as many new triangles as there as sides.
Each such triangle has an area 9 times smaller than the triangle it's built on.
Therefore, the total area is obtained by adding a geometric series to the area of
the original triangle (used as unit ot area):



